Find the unknown values in the problem involving trigonometry graphs

[chwala]

Homework Statement

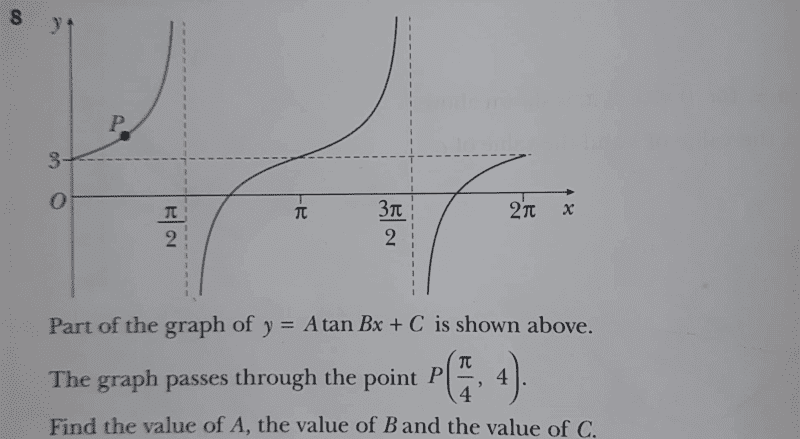
see attached

Relevant Equations

trigonometry

My interest is on finding the value of $A$ only. From my calculations, $A=1$and not $2$ as indicated on textbook solution.
In my working we have; i.e $4=A +3.$
The values of $B$and $C$ are correct though. Kindly advise.

Find the question and textbook solution.

 

[BvU]

In my working

Which you don't post, so we depend on telepathy now.

But I suppose my answer would also be $A=1$

$\$

 

[chwala]

Ok I will indeed post my working later. I'll get back on this..finishing on some chores @BvU

 

[chwala]

For tangent graphs, the period is given by;
$Bx= π$,
the period of the given graph is $x$=$\dfrac {3π}{2}-\dfrac {π}{2}= π$
therefore,
$Bπ= π$, →$B=1$,
The principal axis crosses the y-axis at the point $(0,3)$, therefore $C=3$.
Using the given point $P\left [\frac{π}{4},4\right]$, we shall have,
$y=A tan Bx + C$
$4=A tan \dfrac {π}{4}+3$
$4=A+3$
$A=1$

 

[Mark44]

I agree as well that A = 1. The graph of $y = 2\tan(x) + 3$ would pass through the point $(\pi/4, 5)$ rather than the point P shown on the graph. Also, I find it odd that the problem parameters are A, B, and C, but the posted answer uses a, b, and c. That's sloppy.