Find the unkown tensions and masses in the situation below

[Venturi365]

TL;DR Summary: I don't know if my procedure is correct in this excercise

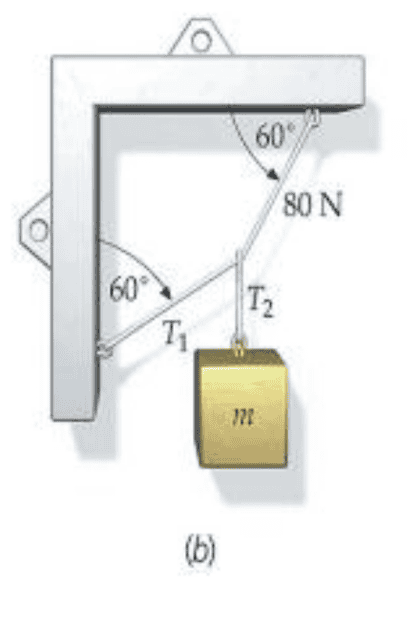
I've tried to solve this problem but I find my solution unintuitive and I think I might be wrong.

First of all, applying Newton's Laws I calculated the value for $T_1$ like this:

$$
\begin{align}
\sum F_{x} &=0\\
\sin(60) \cdot T_{1}+80\, \mathrm{N}\cdot \cos(60) &=0\\
T_{1}&=\frac{-80\cdot\cos(60)}{\sin(60)}\\
T_{1} &\approx -46,2\, \mathrm{N}
\end{align}
$$

Here's the first thing that looks odd to me, because intuitively $T_{1}$ should be $80\,\mathrm{N}$ too, but It may be just a wrong hypothesis.

Then I apply the same law to the node of the three cords:

$$
\begin{align}
\sum F_{y}&=0\\
T_{1}\cdot\cos(60)+80\,\mathrm{N}\cdot\sin(60)+T_{2}&=0\\
T_{2}&=46,2\,\mathrm{N}\cdot\cos(60)-80\,\mathrm{N}\cdot\sin(60)\\
T_{2}&\approx -46,2\,\mathrm{N}
\end{align}
$$

Which is the same force as $T_{1}$. Is my method ok or am I wrong at some point?

 

[Lnewqban]

Welcome, @Venturi365 !
What is the wording of this problem?

 

[Venturi365]

Welcome, @Venturi365 !
What is the wording of this problem?

It asks you to find the values of $T_{1}$, $T_{2}$ and $m$ supposing that the cables have no mass and that $g=9,81\,\mathrm{\frac{m}{s^{2}}}$. The wording is just as I wrote it in the title.

 

[Lnewqban]

Could you do a free body diagram for the node of the three cords?
Consider that the node must have a balance of horizontal and vertical forces.
The magnitude of T1 does not need to be 80 Newtons (imagine the extreme case in which the right half of the rope becomes vertical and its tension is equal to mg).

 

[haruspex]

Which is the same force as T1.

The three forces must balance at the joint. Therefore the resultant of T1 and T2 must be along the line of 'T3'. With these angles, that means it lies on the bisector of the angle between them, implying they are of equal magnitude.

Btw, I find your use of signs quirky. A tension is generally taken to be a magnitude. (You could adopt a convention in which tensions have one sign and compressions the other.) Here, your equations have T1 and T2 negative but T3 positive.

I guess that came from starting with the vectors form, but then you should have measured all angles from the same reference direction, making some trig values negative.

 

[Venturi365]

The three forces must balance at the joint. Therefore the resultant of T1 and T2 must be along the line of 'T3'. With these angles, that means it lies on the bisector of the angle between them, implying they are of equal magnitude.

Btw, I find your use of signs quirky. A tension is generally taken to be a magnitude. (You could adopt a convention in which tensions have one sign and compressions the other.) Here, your equations have T1 and T2 negative but T3 positive.

I guess that came from starting with the vectors form, but then you should have measured all angles from the same reference direction, making some trig values negative.

Taking all that in consideration I get the same result:

First I find $T_{1}$ knowing that, at the joint, there's an equilibrium in the $x$ axis in which $T_{2}$ doesn't participate (now with the angles corrected):

$$
\begin{align}
\sum F_{x} & =0 \\
\cos \left(30^\circ\right) ·T_{1}+\cos \left(180^\circ+60^\circ\right) ·80\,\mathrm{N} & =0 \\
\frac{\sqrt{ 3 }}{2}·T_{1}-\frac{1}{2}80\,\mathrm{N} & =0 \\
T_{1} & =\frac{80}{\sqrt{ 3 }} \\
T_{1} & \approx 46,18\,\mathrm{N}
\end{align}
$$

Then, I sum all the tensions in the $y$ axis:

$$
\begin{align}
\sum F_{y} & =0 \\
T_{1}·\sin \left(30^\circ\right) +T_{2}+80\,\mathrm{N}·\sin \left(180^\circ+60^\circ\right) & =0 \\
\frac{80}{2\sqrt{ 3 }}+T_{2}-\frac{80\sqrt{ 3 }}{2 } & =0 \\
T_{2} & =\frac{80\sqrt{ 3 }}{2}-\frac{80}{2\sqrt{ 3 }} \\
T_{2} & \approx 46,18\,\mathrm{N}
\end{align}
$$

And there it is, the same solution, maybe I'm just right and I'm being a paranoid, idk.

I'll calculate the mass, just for fun:

$$
\begin{align}
w & =T_{2} \\
mg & =46,18 \\ \\

& \to \boxed{\; g =9,18\,\mathrm{\frac{m}{s^{2}}} \;} \\ \\

m & =\frac{46,18}{9,18} \\
m & \approx 5,03\,\mathrm{kg}
\end{align}
$$

Thx for the signs advice, I didn't see that.

 

[haruspex]

And there it is, the same solution, maybe I'm just right and I'm being a paranoid

I explained in post #5 that with the angles specified it was inevitable the two tensions would be the same.

 

[Venturi365]

I explained in post #5 that with the angles specified it was inevitable the two tensions would be the same.

Oh, yeah, I'm so sorry. I've been studying for a long time and rn is 3 am in Spain so my brain didn't translate that correctly, lmao.

Thank you for your patience and taking the time to answer :)

 

[haruspex]

Oh, yeah, I'm so sorry. I've been studying for a long time and rn is 3 am in Spain so my brain didn't translate that correctly, lmao.

Thank you for your patience and taking the time to answer :)

No problem, you are welcome.