Find the velocity and angular velocity of the rod and point

[Noob of the Maths]

Homework Statement

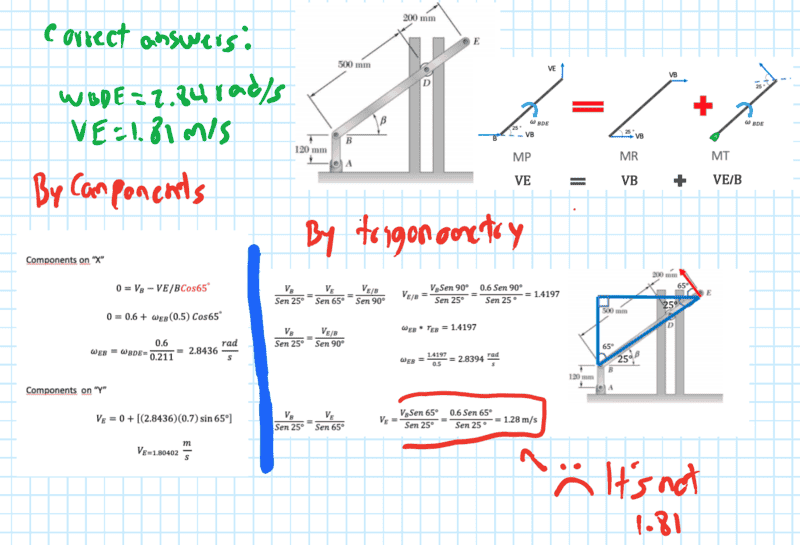
Rod BDE is partially guided by a roller at D which moves in a vertical track. Knowing that at the instant shown the angular velocity of crank AB is 5 rad/s clockwise and that °β=25° ,determine (a) the angular velocity of the rod, (b) the velocity of Point E.

Relevant Equations

WED * rED...

Hi everyone :)!

I resolve this problem with components method and trigonometry method.

My results with components method its okay, but i can´t obtain the correct VE velocity.

Im sure that the problem its in the angles, but i don't know how to fix it.

The correct answers:

-Angular velocity of the rod: 2.84 rad/s
-Velocity of Point E: 1.81 m/s

In trigonometry i obtain 1.28 m/s ;(

Thanks for your time!

 

[Lnewqban]

I would calculate the velocity of point D, which can only be vertical up.
The magnitude and direction of the velocity of point E depends directly on Vb and Vd.

The vertical component of Ve should be greater than Vd in a factor of 700/500, as they both, points D and E, move up while point B can only instantaneously move horizontally.

The horizontal component of Ve should be smaller than Vb in a factor of 200/500, as they both, point B and E, get closer to the vertical line of point D, but at different rates of speed.

The vectorial summation of the x and y components of Ve, should produce 1.81 m/s.

 

[Noob of the Maths]

I would calculate the velocity of point D, which can only be vertical up.
The magnitude and direction of the velocity of point E depends directly on Vb and Vd.

The vertical component of Ve should be greater than Vd in a factor of 700/500, as they both, points D and E, move up while point B can only instantaneously move horizontally.

The horizontal component of Ve should be smaller than Vb in a factor of 200/500, as they both, point B and E, get closer to the vertical line of point D, but at different rates of speed.

The vectorial summation of the x and y components of Ve, should produce 1.81 m/s.

Yes, i obtain 1.81 in the summation of components. But this result its not the same in the trigonometry comprobation

 

[Lnewqban]

Yes, i obtain 1.81 in the summation of components. But this result its not the same in the trigonometry comprobation

Following my reasoning of previous post, I see no way to justify the relations among velocities and angles that you have shown in your trigonometry method.

From the point of view of an observer standing on the ground, point B moves horizontally to the right, point D moves vertically up, a middle point located between B and D moves to the right and up diagonally.

Therefore, point E moves to the left and up, but at an angle with the horizontal that must be greater than the assumed 65 degrees.

 

[Noob of the Maths]

Following my reasoning of previous post, I see no way to justify the relations among velocities and angles that you have shown in your trigonometry method.

From the point of view of an observer standing on the ground, point B moves horizontally to the right, point D moves vertically up, a middle point located between B and D moves to the right and up diagonally.

Therefore, point E moves to the left and up, but at an angle with the horizontal that must be greater than the assumed 65 degrees.

Yes, previous reasoning was wrong.

I asked for help to my teacher, and he just say: "you may first need to know the speed of D..."

So, I performed another procedure based on distances and prime.

But... I arrive at an equation that does not work for me because I already know the velocity of B... ;(

Im stuck with the trigonometry comprobation of velocity on E point...

 

[Lnewqban]

"... the angular velocity of crank AB is 5 rad/s clockwise." :)

Again, you should consider the geometry of the mechanism.
Section BD behaves like a ladder sliding on a horizontal grade and a vertical wall of a building.
Section DE is just like an extension of that imaginary ladder; therefore, the movement of point E respect to the grade is going to be magnified (700 mm/500 mm) respect to the combined movements of points B and D.

 

[Noob of the Maths]

"... the angular velocity of crank AB is 5 rad/s clockwise." :)

Again, you should consider the geometry of the mechanism.
Section BD behaves like a ladder sliding on a horizontal grade and a vertical wall of a building.
Section DE is just like an extension of that imaginary ladder; therefore, the movement of point E respect to the grade is going to be magnified (700 mm/500 mm) respect to the combined movements of points B and D.

View attachment 290148

then all this time I got the speed of VD (1.28 m/s) :O? Now I just need to use this velocity and take its angular velocity, in order to calculate the velocity of VE? just as it was done with the velocity of B...

 

[Lnewqban]

then all this time I got the speed of VD (1.28 m/s) :O? Now I just need to use this velocity and take its angular velocity, in order to calculate the velocity of VE? just as it was done with the velocity of B...

 

[Noob of the Maths]

"... the angular velocity of crank AB is 5 rad/s clockwise." :)

Again, you should consider the geometry of the mechanism.
Section BD behaves like a ladder sliding on a horizontal grade and a vertical wall of a building.
Section DE is just like an extension of that imaginary ladder; therefore, the movement of point E respect to the grade is going to be magnified (700 mm/500 mm) respect to the combined movements of points B and D.

View attachment 290148

using as a reference other problems I saw, the vectors drawn on the diagrams could already be considered a check, something like: when the velocities of the midpoint and the velocity Vb are equal, the omega is zero.

my problem is just the sum of the VE vectors. I could do it using the velocity and angular velocity of B (as I show in the first one), but implementing that with VE causes me problems ;(.

Seeing the rectangular vector of VE, I suppose that an angle of 90 would be used, since the relative velocity is perpendicular to the rod.

This showed me that I am still a dumb in this cases...

 

[Lnewqban]

using as a reference other problems I saw, the vectors drawn on the diagrams could already be considered a check, something like: when the velocities of the midpoint and the velocity Vb are equal, the omega is zero.

my problem is just the sum of the VE vectors. I could do it using the velocity and angular velocity of B (as I show in the first one), but implementing that with VE causes me problems ;(.

Seeing the rectangular vector of VE, I suppose that an angle of 90 would be used, since the relative velocity is perpendicular to the rod.

This showed me that I am still a dumb in this cases...

90 degrees is not the angle because the rod does not rotate around any fixed pivot.
Both pivot points, B and D, have rectilinear movements, and that affects all the points along the rod in a different manner.

If point B is moving towards the vertical line that is the trajectory of point D, then point E must also move towards that line (although at a different instantaneous velocity, due to the whole geometry of the mechanism); hence, the vector Vex towards the left.

If point D is moving up and away from the horizontal line that is the trajectory of point B, then point E must also move up and away from that line (although at a greater instantaneous velocity that D, due to the whole geometry of the mechanism); hence, the vertical vector Vey pointing up.

Combining the values of Vex and Vey and using Pitagora's equation (only because the trajectories of points B and D happen to be perpendicular to each other), we obtain the Ve vector (which is not perpendicular to the rod for any reason).

You are not dumb, my friend; you are just trying to learn difficult things.

 

[Noob of the Maths]

90 degrees is not the angle because the rod does not rotate around any fixed pivot.
Both pivot points, B and D, have rectilinear movements, and that affects all the points along the rod in a different manner.

If point B is moving towards the vertical line that is the trajectory of point D, then point E must also move towards that line (although at a different instantaneous velocity, due to the whole geometry of the mechanism); hence, the vector Vex towards the left.

If point D is moving up and away from the horizontal line that is the trajectory of point B, then point E must also move up and away from that line (although at a greater instantaneous velocity that D, due to the whole geometry of the mechanism); hence, the vertical vector Vey pointing up.

Combining the values of Vex and Vey and using Pitagora's equation (only because the trajectories of points B and D happen to be perpendicular to each other), we obtain the Ve vector (which is not perpendicular to the rod for any reason).

You are not dumb, my friend; you are just trying to learn difficult things.

After the analysis with the diagrams, I think it would be easy to demonstrate trigonometrically with the "image" method.

Its right? ;(