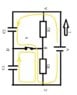
- #1
Helly123
- 581
- 20
Homework Statement
C1 = 4 micro F
C2 = 8 mF
R1 = 4 ohm
R2 = 8 ohm
V = 12
Questions :
1) Find current I when S not closed
2) find Vb, when Vc is 0
3) find Vd, when Vc is 0
4) total charge move from B to D
C2 = 8 mF
R1 = 4 ohm
R2 = 8 ohm
V = 12
Questions :
1) Find current I when S not closed
2) find Vb, when Vc is 0
3) find Vd, when Vc is 0
4) total charge move from B to D
Homework Equations
Vf - Vi = F.d/q
(not sure this below is useful equations)
I = E/Z
E = E resistor = E capacitor
I total = Iresistor + Icapacitor
z = 1/(1/Zr + 1/Zc)
The Attempt at a Solution
1) I = V/R = 12/12 = 1A. (I wonder if the capacitor will affect current? since in Q = CV, there is no current as in V= IR)
2) what makes the Vc is 0? I thought that Vb = 12 V - ## V_{resistor2ohm}## Is there any relation with Vc?
3) same as 2)
4) I thought maybe the charge referred is the charge in this equations (Vf - Vi) = F.d/q
any help is appreciated :)