- #1
- 1,753
- 143
The region bounded by the curves is rotated about the specified axis. Find the volume of th eresulting solid by and method.
[tex]x^2 + \left( {y - 1} \right)^2 = 1[/tex]
First question want it rotated about the x-axis, the second question wants it rotated about the y-axis.
So I re-write it in terms of x. Seems easier than in terms of y since there's only 1 x term.
[tex]x = \sqrt { - y^2 + 2y}
[/tex]
The problem is when I graph it,
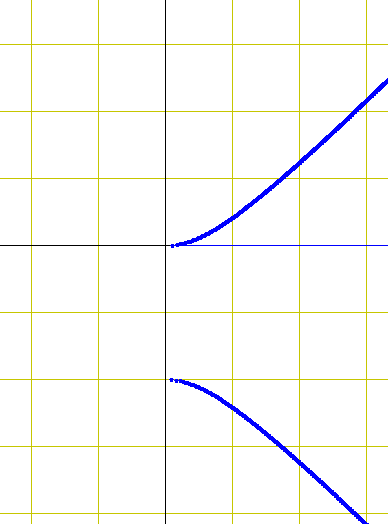
So nothing is bounded. There is no solid to rotate. Should I have solved in terms of y instead? How would I do that?
[tex]x^2 + \left( {y - 1} \right)^2 = 1[/tex]
First question want it rotated about the x-axis, the second question wants it rotated about the y-axis.
So I re-write it in terms of x. Seems easier than in terms of y since there's only 1 x term.
[tex]x = \sqrt { - y^2 + 2y}
[/tex]
The problem is when I graph it,
So nothing is bounded. There is no solid to rotate. Should I have solved in terms of y instead? How would I do that?
Last edited: