Find the volume of the parallelepiped

[chwala]

Homework Statement

see attached

Relevant Equations

vector calculus

Am refreshing on this; see attached below

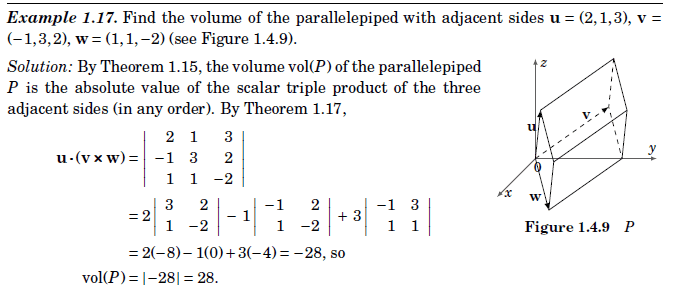ok we can also use the form $[i×j=k, k×i=j , j×k=i]$ right?

to give us say, $w⋅(u ×v)=v⋅(w ×u)$ in realizing same solution.

 

[sysprog]

Please elaborate on what you mean by "the form $[i×j=k, k×i=j , j×k=i]$".

 

[chwala]

I wanted to indicate,
For any vectors in 3-dimensional space it follows that,
$w⋅(u ×v)=v⋅(w ×u)=u⋅(v ×w)$... yap with this, i should realize the same value of the required volume... the form $[i×j=k, k×i=j , j×k=i]$ is not applicable here...

 

[sysprog]

the form $[i×j=k, k×i=j , j×k=i]$ is not applicable here...

Thank you for your reply.

 

[chwala]

Nice sysprog...I am refreshing on this area, its long since I looked at vector calculus...of course I should be able to check and prove (some of the questions that I ask) the concept given, I just want to be certain that it's mathematically acceptable from the great minds here...cheers

 

[sysprog]

It seems to me that you're trying to solidify your understanding of the relation that the dot product has to the cross product.

It's true that if $u$, $v$ and $w$, are vectors in 3-space, then $w · (u × v) = v · (w × u) = u · (v × w)$.

Interchanging two rows changes the sign of a determinant, so interchanging two rows twice results in the same-sign determinant.