Find the volume of the solid of revolution, or state that it does not exist. #2

In summary, the student is having trouble with finding the volume of a solid of revolution and is looking for help. The region bounded by f(x)= 6(4-x)^(-1/3) and the x-axis on the interval [0,4) is revolved avout the y-axis. The student can use a function plotter to see the graph on the indicated interval. The student can either use the shell method or the washer method to find the volume. The student starts by computing the element of the volume and then integrates.
  • #1
abc1
9
0
I'm having some trouble with this problem:

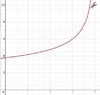
Find the volume of the solid of revolution, or state that it does not exist. The region bounded by f(x)= 6(4-x)^(-1/3) and the x-axis on the interval [0,4) is revolved avout the y-axis.

How would I be able to tell whether to use the shell, disk, or washer method?
 
Physics news on Phys.org
  • #2
We can use a function plotter to see the graph on the indicated interval:

View attachment 2238

Looks to me like I would try the shell method. Can you state the volume of an arbitrary shell?
 

Attachments

  • abc.jpg
    abc.jpg
    16.5 KB · Views: 52
  • #3
How can I tell that I have to use the shell method?

Would the formula for this be 2pi times the integral from 0 to 4 of x* (6(4-x)^(-1/3) dx ?

So then, how would I take the limit of this? What test should I use?
 
  • #4
abc said:
How can I tell that I have to use the shell method?

Would the formula for this be 2pi times the integral from 0 to 4 of x* (6(4-x)^(-1/3) dx ?

So then, how would I take the limit of this? What test should I use?

You don't have to use the shell method, but can you see that the shell method allows for the computation of the volume as a single integral whereas the washer method will require an integral to be added to a cylinder? Either way would work though. In fact, I recommend to students to use more than one method both as a check as for the practice.

I always like to start by computing an element of the volume and then integrating. It appears that you do have the correct integral representing the volume. I think first though, I would use the substitution:

\(\displaystyle u=4-x\)

What do you have now?
 
  • #5
Would it be 2pi times the integral from 0 to 4 of x* -(6(u)^(-1/3) du ?
 
  • #6
abc said:
Would it be 2pi times the integral from 0 to 4 of x* -(6(u)^(-1/3) du ?

You want to write that $x$ out front in terms of $u$...:D
 
  • #7
so the limit as u approaches infinity from 4 to 0 of 2pi times the integral from 0 to 4 of (4-x)* -(6(u)^(-1/3) du since we have to rewrite the limits of integration as well because of the u-substitution?
 

1. What is the solid of revolution?

The solid of revolution is a three-dimensional figure created by rotating a two-dimensional shape around an axis, such as a line or curve. This results in a solid shape with a circular cross-section.

2. How do you find the volume of a solid of revolution?

To find the volume of a solid of revolution, you can use the formula V = π∫(R(x))^2 dx, where R(x) is the radius of the cross-section at a given point along the axis of rotation and the integral is taken over the interval of rotation. This formula is derived from the disk method in calculus.

3. Can the volume of a solid of revolution be negative?

No, the volume of a solid of revolution cannot be negative. This is because volume is a measure of space and cannot have a negative value. However, the volume can be equal to zero if the solid of revolution does not have any volume, such as a flat shape being rotated around an axis.

4. In what cases would the volume of a solid of revolution not exist?

The volume of a solid of revolution does not exist when the shape being rotated has a hole or empty space in the center, as this would result in a hollow solid with no volume. Additionally, if the shape being rotated does not have a continuous cross-section, the volume cannot be calculated.

5. Can you find the volume of a solid of revolution for any shape?

No, the volume of a solid of revolution can only be found for shapes that have a circular cross-section. This includes shapes such as circles, ellipses, and certain types of curves. The shape must also have a continuous cross-section in order for the volume to be calculated accurately.

Similar threads

Volumes of solids of revolution
    • Calculus
Replies
11
Views
2K
MHB Good day, Exam Integrals: volume and area
    • Calculus
Replies
4
Views
750
MHB Find the volume of the solid of revolution, or state that it does not exist.
    • Calculus
Replies
7
Views
3K
I How to apply the disk/washer and shell methods
    • Calculus
Replies
1
Views
1K
I Confusion on the Volumes of Solids of Revolution
    • Calculus
Replies
3
Views
1K
MHB What is the Volume of a Solid with Squares as Cross Sections?
    • Calculus
Replies
2
Views
1K
MHB Triple Integrals: Finding Volume of Solid S Bounded by Planes
    • Calculus
Replies
5
Views
1K
I Volume of Solid of Revolution (About the line y = x)
    • General Math
Replies
6
Views
1K
MHB Integration application: solids of revolution
    • Calculus
Replies
13
Views
3K
MHB 18 Find the volume of the solid generated by revolving the region about y-axis.
    • Calculus
Replies
4
Views
1K

Hot Threads

Recent Insights

Back
Top