MatinSAR
- 673
- 204
- Homework Statement
- Find thermal capacity of vander waals gas.
- Relevant Equations
- Tds equations.
Can anyone guide me how can I find ##C_P## and ##C_V##?
There are two equations in my book which I think can help but I'm not sure if I can use them to find ##C_P## and ##C_V## of a vander waals gas.


I know equation of state of this gas.
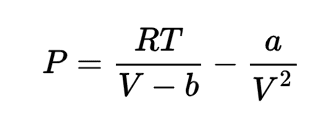
There are two equations in my book which I think can help but I'm not sure if I can use them to find ##C_P## and ##C_V## of a vander waals gas.
I know equation of state of this gas.