Find $\theta$ for Trig Function 33: No Calculator

[bergausstein]

33. find two values of $\theta$ , $0^{\circ} <\theta<360^{\circ}$ that
satisfy the given trigonometric equation. without using calculator.

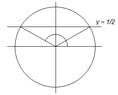
a. $\displaystyle \sin\theta=\frac{1}{2}$

b. $\displaystyle \cos\theta=-\frac{\sqrt{3}}{2}$

c. $\displaystyle \csc\theta=-\sqrt{2}$

 

[MarkFL]

These questions rely on your knowing the values of certain "special" angles for the trig. functions, and possibly the identities:

\(\displaystyle \sin(\pi-\theta)=\sin(\theta)\)

\(\displaystyle \cos(2\pi-\theta)=\cos(\theta)\)

For part c), I would invert both sides of the equation to get:

\(\displaystyle \sin(\theta)=-\frac{1}{\sqrt{2}}\)

Let's begin with part a). In which quadrants do you expect to find solutions?

 

[bergausstein]

in part a. $\displaystyle 30^{\circ}$ would satisfy the equation. but i know it's not only the answer. can you help me to find the other.

 

[SuperSonic4]

in part a. $\displaystyle 30^{\circ}$ would satisfy the equation. but i know it's not only the answer. can you help me to find the other.

$\displaystyle 30^{\circ}$ is indeed one of the solutions (in fact it's the principal one)

A good place to start is working out where $\sin(\theta) > 0$ so you can narrow your search.

The basic definition of $\sin(\theta) = \dfrac{Opp}{Hyp}$. When this is applied to the unit circle you can say that $\sin(\theta) = y$ (because r=1)

Therefore for $\sin(\theta) > 0$ it follows that $y > 0$.

Now in which quadrant(s) is/are $ y > 0$

---

edit:

Alternatively if you know your graph of $f(\theta) = \sin(\theta)$ you can see that $ \displaystyle f(0) = 0 \ ,\ f(90^o) = 1\ ,\ f(180^o) = 0\ ,\ f(270^o) = -1 \text{ and }\ f(360^o) = 0$

This tells you there are two solutions: one between 0 and 90 which is the 30 you found and one between 90 and 180.

 

[MarkFL]

Here's another way to approach it...draw a unit circle and the line $y=\dfrac{1}{2}$, and then draw rays from the origin to the two points where the line intersects the circle, then what are the terminal angles associated with the two rays?

View attachment 1216

The other questions can be done similarly, using vertical lines for the cosine function. This is how I often visualize such problems.

 

[bergausstein]

but how would i know the measure of that other angle? what method should i use to determine its measure?

 

[MarkFL]

The angle on the right, the smaller angle is $0^{\circ}+30^{\circ}$ and so you should be able to see the larger angle is $180^{\circ}-30^{\circ}$.

This is closely related to the identity I gave in my first post:

\(\displaystyle \sin(\pi-\theta)=\sin(\theta)\)

Think of two particles on the unit circle, the first at (1,0) and the second at (-1,0). The first moves counter-clockwise at a constant rate, and its $y$ coordinate is $y=\sin(\theta)$. The second moves at the same rate but in the clockwise direction, and its $y$-coordinate is given by $y=\sin(\pi-\theta)$. Can you see that their $y$-coordinates are the same for all $\theta$? This is how I visualize the identity above.

Can you use the two particle model to visualize the identity I gave in my first post for the cosine function?