chwala
Gold Member
- 2,827
- 415
- Homework Statement
- Find vector ##x## and ##y## by considering the vector diagram
- Relevant Equations
- Vectors
This is the problem,
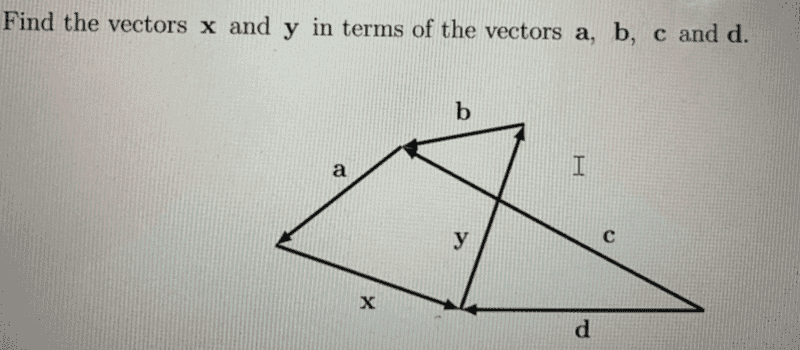
I managed to solve it, i just want to check if there is an alternative approach. Find my solution below;
##\vec x= -\vec a-\vec b-\vec y##
##\vec y= -\vec d+\vec c-\vec b## therefore,
##\vec x= -\vec a-\vec b+\vec d-\vec c+\vec b##
##\vec x= -\vec a+\vec d-\vec c##
I managed to solve it, i just want to check if there is an alternative approach. Find my solution below;
##\vec x= -\vec a-\vec b-\vec y##
##\vec y= -\vec d+\vec c-\vec b## therefore,
##\vec x= -\vec a-\vec b+\vec d-\vec c+\vec b##
##\vec x= -\vec a+\vec d-\vec c##