MHB Find Where Two Tangent Lines Intersect on a Circle | Math Help

[MarkFL]

Here is the question:

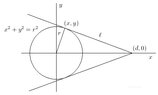
How can i find where two tangent lines intersect on a circle?

I need math help tonight. Is there a process i need to follow to find out where the lines meet?

I have posted a link there to this topic so the OP can see my work.

 

[MarkFL]

Hello Getty,

We can greatly simplify this problem, if we orient the circle's center at the origin of our coordinate system, and rotate the circle such that the two tangent points have the same $x$-coordinate (where $0<x<r$), one point in the first quadrant, and one in the fourth quadrant.

Please refer to the following diagram:

View attachment 1164

Because $r$ and $\ell$ are perpendicular, we may state:

$$r^2+\ell^2=d^2$$

Using the distance formula, we find:

$$\ell^2=(x-d)^2+y^2$$

and from the equation of the circle, we have:

$$y^2=r^2-x^2$$

Hence, we may now write:

$$r^2+(x-d)^2+r^2-x^2=d^2$$

$$2r^2+x^2-2xd+d^2-x^2=d^2$$

$$r^2-xd=0$$

$$d=\frac{r^2}{x}$$