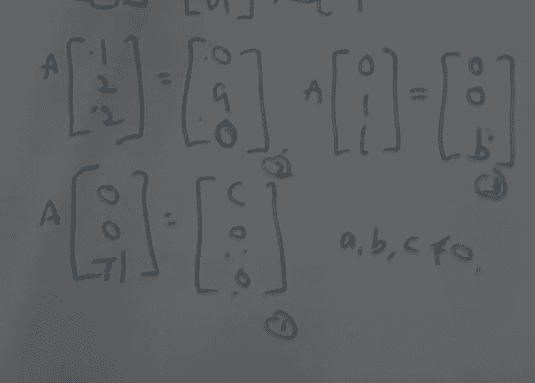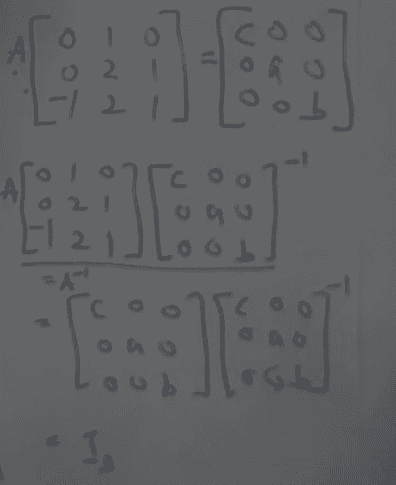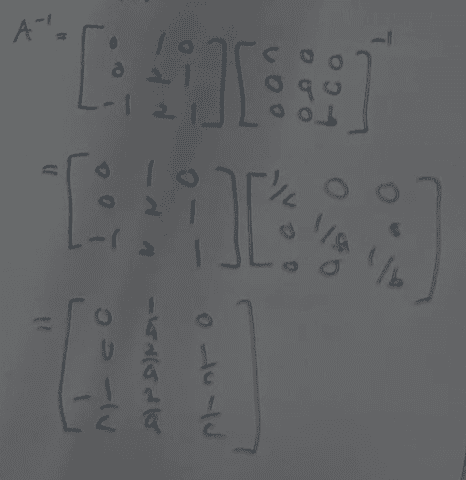Finding ##A^{-1}## of a matrix given three submatrices

[member 731016]

Homework Statement

Please see below

Relevant Equations

Please see below

For this problem,
Find $A^{-1}$ given,

The solution is,

However, in the first image, why are we allowed to put together the submatrices in random order? In general does someone please know why we are allowed to decompose matrices like this?

Many thanks!

 

[Structure seeker]

Homework Statement: Please see below
Relevant Equations: Please see below

why are we allowed to put together the submatrices in random order?

From three instances of $Ax=b$ for x and b vectors, you just put the three equations in a row of 3 to get the matrices B and C with $AB=C$. You are thus given a matrix multiplication equation. Then you use the properties of this multiplication: $AB=C$ implies $B^{-1}A^{-1}=C^{-1}$ implies $A^{-1}=BC^{-1}$. We might transform B and C with a column permutation by right-multiplying with a permutation matrix, in fact with any invertible matrix M. Then we get $ABM=CM$ implies $A^{-1}=BM(CM)^{-1}=BMM^{-1}C^{-1}=BC^{-1}$

 

[Structure seeker]

So the point is that $Ax=b$ comma $Ay=c$ may also be written as $A(x ~ y) = (b ~ c)$. This is a property of matrices

 

[anuttarasammyak]

There are six ways of forming matrices as you say. Choose one of them,e.g.

When you multiply
$$\begin{pmatrix} 0 & 1 & 0 \\ 0 & 0 & 1 \\ 1 & 0 & 0 \\ \end{pmatrix}$$
from right on the both sides, you will find that the equation becomes one of another choice and you will know that the both choices are equivalent. You may be able to find all the six matrices to confirm that all the six choices are equivalent.

 

[SammyS]

However, in the first image, why are we allowed to put together the submatrices in random order? In general does someone please know why we are allowed to decompose matrices like this?

Many thanks!

It is not "random order".
They did not decompose a matrix, rather a matrix is being constructed based upon the given information.

As is often the case:
Rather than investigating how that construction works, you just post a solution and ask others to explain the solution.

My suggestion:
Using matrix multiplication verify (for yourself) the first line of the solution.

You can not learn math or physics simply by looking at posted solutions.

 

[PhDeezNutz]

I’d imagine it has something to do with swapping rows and columns in a matrix (elementary row operations or column operations preserve the solution space so you can arrange them however you want)

 

[Steve4Physics]

I think no one has yet pointed out that the solution (2nd image in Post #1) is wrong. It says:

$\begin {bmatrix} 0 & 1 & 0\\ 0 & 2 & 1\\ -1 & 2 & 1 \end {bmatrix} \begin {bmatrix} \frac 1c & 0 & 0\\ 0 & \frac 1a & 0\\ 0 & 0 & \frac 1b \end {bmatrix} = \begin {bmatrix} 0 & \frac 1a & 0\\ 0 & \frac 2a & \frac 1c\\ -\frac 1c & \frac 2a & \frac 1c \end{bmatrix}$

This is clearly wrong as $b$ has disappeared into the aether! It should say:

$\begin {bmatrix} 0 & 1 & 0\\ 0 & 2 & 1\\ -1 & 2 & 1 \end {bmatrix} \begin {bmatrix} \frac 1c & 0 & 0\\ 0 & \frac 1a & 1\\ 0 & 0 & \frac 1b \end {bmatrix} = \begin {bmatrix} 0 & \frac 1a &0\\ 0 & \frac 2a & \frac 1b\\ -\frac 1c & \frac 2a & \frac 1b \end {bmatrix}$

In addition to what has already been said, it appears that the ‘submatrices’ (columns) have not been put together in ‘random order’. They have been put together, for convenience, in the order which creates the diagonal matrix, $diag(c, a, b)$. This is to make finding the inverse of the matrix easy.

 

[Mark44]

It should say:

$\begin {bmatrix} 0 & 1 & 0\\ 0 & 2 & 1\\ -1 & 2 & 1 \end {bmatrix} \begin {bmatrix} \frac 1c & 0 & 0\\ 0 & \frac 1a & 1\\ 0 & 0 & \frac 1b \end {bmatrix} = \begin {bmatrix} 0 & \frac 1a &0\\ 0 & \frac 2a & \frac 1b\\ -\frac 1c & \frac 2a & \frac 1b \end {bmatrix}$

In addition to what has already been said, it appears that the ‘submatrices’ (columns) have not been put together in ‘random order’. They have been put together, for convenience, in the order which creates the diagonal matrix, $diag(c, a, b)$. This is to make finding the inverse of the matrix easy.

Exactly.

To flesh out what @Steve4Physics says above, it's important to have clear, concise equations of the work. It's also extremely important to post legible screen shots. I had a difficult time reading the entries in some of your matrices. The problem with illegible screen shots is why we discourage the use of images for most homework problems.

$A \begin {bmatrix} 0 & 1 & 0\\ 0 & 2 & 1\\ -1 & 2 & 1 \end {bmatrix} = \begin {bmatrix} c & 0 & 0\\ 0 & a & 0\\ 0 & 0 & b \end {bmatrix}$
For the matrix equation above, multiply on the left by $A^{-1}$. It's reasonable to assume this inverse exists, otherwise there's no point to the problem.

This results in the following matrix equation:
$\begin {bmatrix} 0 & 1 & 0\\ 0 & 2 & 1\\ -1 & 2 & 1 \end {bmatrix} = A^{-1} \begin {bmatrix} c & 0 & 0\\ 0 & a & 0\\ 0 & 0 & b \end {bmatrix}$

Now multiply each side of the matrix equation on the right by the inverse of this diagonal matrix. This unnamed matrix on the right is very easy to invert. The entries on the main diagonal of its inverse are 1/c, 1/a, and 1/b, respectively.

$\begin {bmatrix} 0 & 1 & 0\\ 0 & 2 & 1\\ -1 & 2 & 1 \end {bmatrix} \begin {bmatrix} \frac 1c & 0 & 0\\ 0 & \frac 1a & 0\\ 0 & 0 & \frac 1b \end {bmatrix} = A^{-1} I = A^{-1}$

I got the identity matrix in the next-to-last expression when I multiplied the diagonal matrix with entries c, a, and b by its inverse, which is another diagonal matrix with entries 1/c, 1/a, and 1/b.

All that's left to do is to multiply the two matrices on the left side of the equation above, which results in the matrix that @Steve4Physics showed.