Finding $a$ for a Degenerate BFS in Given System of Restrictions

[evinda]

Hello! (Wave)

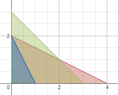
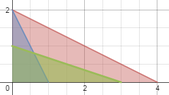
The following system of restrictions is given:$$x_1+ 2 x_2 \leq 4 \\ 2x_1+x_2 \leq 2 \\ x_1+a x_2 \leq 3 \\ x_1, x_2 \geq 0$$
For which values of $a$ is there a degenarate basic feasible solution?

I wrote the above system of restrictions in canonical form as follows:$$x_1+ 2 x_2 +x_3= 4 \\ 2x_1+x_2 +x_4= 2 \\ x_1+a x_2 + x_5= 3 \\ x_1, x_2 , x_3, x_4, x_5\geq 0$$$$A=\begin{bmatrix}
1 & 2 & 1 & 0 & 0\\
2 & 1 & 0 & 1 & 0\\
1 & a & 0 & 0 & 1
\end{bmatrix}$$

The order of $A$ is $3$.I thought that for example for $x_1=x_2=0$ we get the non-degenerate basic feasible solution $(0,0,4,2,3)$.
Do we have to find an other non-degenerate basic feasible solution with a common component as the above one so that their subtraction gives a degenerate basic feasible solution? (Thinking)
How can we find an appropriate $a$? (Thinking)

 

[I like Serena]

Hey evinda! (Smile)

What does it mean if we have a degenerate basic feasible solution? (Wondering)

 

[evinda]

Hey evinda! (Smile)

What does it mean if we have a degenerate basic feasible solution? (Wondering)

A non-degenare basic feasible solution is a basic feasible solution with exactly $r(A)=m$ non-zero components.

That's why I thought that a degenerate basic feasible solution is a basic feasible solution with less than $m$ non-zero components.

Am I wrong? (Thinking)

 

[I like Serena]

A non-degenare basic feasible solution is a basic feasible solution with exactly $r(A)=m$ non-zero components.

That's why I thought that a degenerate basic feasible solution is a basic feasible solution with less than $m$ non-zero components.

Am I wrong? (Thinking)

That is correct. (Nod)
Moreover, it is equivalent with having an equation that has a right-hand-side of zero.
And it is also equivalent with having 3 boundary conditions that intersect in the same feasible point. (Nerd)

One way to find it, is to make a drawing, which will reveal where and when degeneracy can happen.
Alternatively, I think we have to walk through all possible basic feasible solutions to see if any of them satisfies the criteria. (Sweating)

 

[evinda]

Moreover, it is equivalent with having an equation that has a right-hand-side of zero.
And it is also equivalent with having 3 boundary conditions that intersect in the same feasible point. (Nerd)

Could you explain it further to me? (Thinking)

One way to find it, is to make a drawing, which will reveal where and when degeneracy can happen.

If we make a drawing what $a$ do we pick?

Alternatively, I think we have to walk through all possible basic feasible solutions to see if any of them satisfies the criteria. (Sweating)

You mean that we run the simplex method till we find a possible degenerate basic feasible solution? (Thinking)

 

[I like Serena]

Could you explain it further to me? (Thinking)

If we make a drawing what $a$ do we pick?

You mean that we run the simplex method till we find a possible degenerate basic feasible solution? (Thinking)

Let's say both $a=1$ and $a=2$.
And yes, we can run the simplex method in different directions until we find a possible degenerate solution.

Let's get back to the explanation once we got something that looks like a degenerate basic feasible solution. (Thinking)

 

[evinda]

And yes, we can run the simplex method in different directions until we find a possible degenerate solution.

The first tableau is:

$\begin{matrix}
B & b & P_1 & P_2 & P_3 & P_4 & P_5 & \theta & \\
P_3 & 4 & 1 & 2 & 1 & 0 & 0 & 2 & L_1\\
P_4 & 2 & 2 & 1 & 0 & 1 & 0 & 2 & L_2\\
P_5 & 3 & 1 & a & 0 & 0 & 1 & \frac{3}{a} & L_3
\end{matrix}$

We choose $P_2$ to get in the basis and we assume that $a \neq 0$.

$$\theta_0=\min \{ 2,2, \frac{3}{a} \}=\frac{3}{a}$$

assuming that $\frac{3}{a} \leq 2$.

The pivot is the element $a$ and so $P_5$ gets out of the basis.

We get the following tableau:$\begin{matrix}
B & b & P_1 & P_2 & P_3 & P_4 & P_5 & \theta & \\
P_3 & 4-\frac{6}{a} & 1-\frac{2}{a} & 0 & 1 & 0 & -\frac{2}{a} & & L_1'=L_1-2L_3'\\ \\
P_4 & 2-\frac{3}{a} & 2-\frac{1}{a} & 0 & 0 & 1 & -\frac{1}{a} & & L_2'=L_2-L_3'\\ \\
P_2 & \frac{3}{a} & \frac{1}{a} & 1 & 0 & 0 & \frac{1}{a} & & L_3'=\frac{L_3}{a}
\end{matrix}$

We have a degenerate basic feasible solution if $4-\frac{6}{a}=0$ or $2-\frac{3}{a}=0$.
Both of the above equalities give $a=\frac{3}{2}$.

But how can we find all $a$ s for which we have a degenerate basic feasible solution? (Thinking)

 

[I like Serena]

We have a degenerate basic feasible solution if $4-\frac{6}{a}=0$ or $2-\frac{3}{a}=0$.
Both of the above equalities give $a=\frac{3}{2}$.

But how can we find all $a$ s for which we have a degenerate basic feasible solution? (Thinking)

Good! (Nod)
To find all $a$ we to assume that either $a < \frac 32$ or $a > \frac 32$ and we need to keep going... (Sweating)

 

[evinda]

Good! (Nod)
To find all $a$ we to assume that either $a < \frac 32$ or $a > \frac 32$ and we need to keep going... (Sweating)

For $a> \frac{3}{2}$ we continue the algorithm.
We choose $P_5$ to get in the basis. The pivot is $\frac{1}{a}$ so $P_2$ gets out of the basis.
Then we get the same tableau as the initial one, so in this case the algorithm terminates.
Right?

If $\frac{3}{a}>2$ then $\theta_0=2$.
The pivot is $2$ and so $P_3$ gets out of the basis.

We get this tableau:

$\begin{matrix}
B & b & P_1 & P_2 & P_3 & P_4 & P_5 & \theta & \\
P_2 & 2 & \frac{1}{2} & 1 & \frac{1}{2} & 0 & 0 & & L_1'=\frac{L_1}{2}\\ \\
P_4 & 0 & \frac{3}{2} & 0 & -\frac{1}{2} & 1 & 0 & & L_2'=L_2-L_1'\\ \\
P_5 & 3-2a & 1-\frac{a}{2} & 0 & -\frac{a}{2} & 0 & 1 & & L_3'=L_3-aL_1'
\end{matrix}$

In this case we get a degenerate basic feasible solution. So do we have to choose now $P_1$ , from the beginning, to get in the basis to check what happens? (Thinking)

 

[I like Serena]

For $a> \frac{3}{2}$ we continue the algorithm.
We choose $P_5$ to get in the basis. The pivot is $\frac{1}{a}$ so $P_2$ gets out of the basis.
Then we get the same tableau as the initial one, so in this case the algorithm terminates.
Right?

Not quite.
We need to walk through all possible basic feasible solutions.
Can't we choose another variable to get in the basis? (Wondering)

If $\frac{3}{a}>2$ then $\theta_0=2$.
The pivot is $2$ and so $P_3$ gets out of the basis.

We get this tableau:

$\begin{matrix}
B & b & P_1 & P_2 & P_3 & P_4 & P_5 & \theta & \\
P_2 & 2 & \frac{1}{2} & 1 & \frac{1}{2} & 0 & 0 & & L_1'=\frac{L_1}{2}\\ \\
P_4 & 0 & \frac{3}{2} & 0 & -\frac{1}{2} & 1 & 0 & & L_2'=L_2-L_1'\\ \\
P_5 & 3-2a & 1-\frac{a}{2} & 0 & -\frac{a}{2} & 0 & 1 & & L_3'=L_3-aL_1'
\end{matrix}$

In this case we get a degenerate basic feasible solution. So do we have to choose now $P_1$ , from the beginning, to get in the basis to check what happens? (Thinking)

We found one! (Nod)
Can we avoid this degenerate basic feasible solution?
Because if we can't, what does that mean? (Wondering)Btw, did you notice that we have a $b$-value of $0$ and that it signifies a degenerate basic feasible solution? (Wondering)

 

[evinda]

Not quite.
We need to walk through all possible basic feasible solutions.
Can't we choose another variable to get in the basis? (Wondering)

We could choose $P_5$ to get in the basis... I will try it right now... (Smirk)

We found one! (Nod)
Can we avoid this degenerate basic feasible solution?
Because if we can't, what does that mean? (Wondering)

We could pick $P_1$ to get in the basis to check what happens. Or not? (Thinking)
I don't really know what it could mean... Could you give me a hint? (Thinking)

Btw, did you notice that we have a $b$-value of $0$ and that it signifies a degenerate basic feasible solution? (Wondering)

Yes, I did... (Nod)

 

[evinda]

If we start with $P_1$, independently of $a$, we get the following tableau:$\begin{matrix}
B & b & P_1 & P_2 & P_3 & P_4 & P_5 & \theta & \\
P_3 & 3 & 0 & \frac{1}{2} & 1 & -\frac{1}{2} & 0 & & L_1'=L_1-L_2'\\ \\
P_1 & 1 & 1 & \frac{1}{2} & 0 & \frac{1}{2} & 0 & & L_2'=L_2-L_1'\\ \\
P_5 & 2 & 0 & a-\frac{1}{2} &0 & -\frac{1}{2} & 1 & & L_3'=L_3-aL_1'
\end{matrix}$

In this case we get a non-degenerate basic feasible solution and so we continue the algorithm, right?

 

[I like Serena]

We could pick $P_1$ to get in the basis to check what happens. Or not? (Thinking)
I don't really know what it could mean... Could you give me a hint? (Thinking)

The problem statement asked for which values of $a$ we get a degenerate basic feasible solution.
We got one for a whole range of values of $a$! (Whew)

If we start with $P_1$, independently of $a$, we get the following tableau:

In this case we get a non-degenerate basic feasible solution and so we continue the algorithm, right?

Yep. (Smirk)

 

[evinda]

Not quite.
We need to walk through all possible basic feasible solutions.
Can't we choose another variable to get in the basis? (Wondering)

If we choose $P_1$ to get in the basis, we find the non-degenerate basic feasible solution $\left( \frac{2-3a}{2-\frac{1}{a}}, \frac{4}{2a-1}, \frac{6a-9}{2a-1},0,0\right)$ . Do we apply again the algorithm? (Thinking)

 

[I like Serena]

If we choose $P_1$ to get in the basis, we find the non-degenerate basic feasible solution $\left( \frac{2-3a}{2-\frac{1}{a}}, \frac{4}{2a-1}, \frac{6a-9}{2a-1},0,0\right)$ . Do we apply again the algorithm? (Thinking)

Is it a feasible solution considering that $a > \frac 32$? (Wondering)

Btw, I suggest to make a drawing. It should clear things up. (Thinking)

 

[evinda]

Is it a feasible solution considering that $a > \frac 32$? (Wondering)

Oh no, it isn't... (Shake)

So, if $\frac{3}{a}>2$ and we choose $P_2$ to get in the basis we find a degenerate basic feasible solution , so we do not have to take other cases. Right? (Thinking)
If $a=\frac{3}{2}$ and we choose again $P_2$ to get in the basis, we get a degenerate basic feasible solution.
By picking $P_2$ to get in the basis we haven't found so far a degenerate basic feasible solution for $a>\frac{3}{2}$.
So do we have to continue for this case the simplex algorithm by putting $P_1$ in the basis?

Btw, I suggest to make a drawing. It should clear things up. (Thinking)

Ok, I will try to... (Nerd)

 

[I like Serena]

Oh no, it isn't... (Shake)

So, if $\frac{3}{a}>2$ and we choose $P_2$ to get in the basis we find a degenerate basic feasible solution , so we do not have to take other cases. Right? (Thinking)
If $a=\frac{3}{2}$ and we choose again $P_2$ to get in the basis, we get a degenerate basic feasible solution.
By picking $P_2$ to get in the basis we haven't found so far a degenerate basic feasible solution for $a>\frac{3}{2}$.
So do we have to continue for this case the simplex algorithm by putting $P_1$ in the basis?

Yep to all. (Smirk)

 

[evinda]

Yep to all. (Smirk)

Having the following tableau$\begin{matrix}
B & b & P_1 & P_2 & P_3 & P_4 & P_5 & \theta & \\
P_3 & 3 & 0 & \frac{1}{2} & 1 & -\frac{1}{2} & 0 & & L_1'=L_1-L_2'\\ \\
P_1 & 1 & 1 & \frac{1}{2} & 0 & \frac{1}{2} & 0 & & L_2'=L_2-L_1'\\ \\
P_5 & 2 & 0 & a-\frac{1}{2} &0 & -\frac{1}{2} & 1 & & L_3'=L_3-aL_1'
\end{matrix}$

we choose either $P_2$ or $P_4$.

If we choose $P_2$ we get the solution $\left( \frac{a-\frac{3}{2}}{a-\frac{1}{2}}, \frac{2}{a-\frac{1}{2}}, \frac{3a-5}{2a-1}\right)$, which is basic feasible degenerate for $a=\frac{5}{3}$. Right?
Now do we have to take again cases? (Thinking)

 

[evinda]

Btw, I suggest to make a drawing. It should clear things up. (Thinking)

How can I make a drawing given that there are 5 unknown variables? (Thinking)

 

[I like Serena]

If we choose $P_2$ we get the solution $\left( \frac{a-\frac{3}{2}}{a-\frac{1}{2}}, \frac{2}{a-\frac{1}{2}}, \frac{3a-5}{2a-1}\right)$, which is basic feasible degenerate for $a=\frac{5}{3}$. Right?
Now do we have to take again cases? (Thinking)

Shouldn't that be $\left( \frac{a-\frac{3}{2}}{a-\frac{1}{2}}, \frac{2}{a-\frac{1}{2}}, \frac{6a-5}{2a-1}\right)$? (Wondering)

If so, when do we get a degenerate case exactly? (Wondering)

 

[I like Serena]

How can I make a drawing given that there are 5 unknown variables? (Thinking)

The original set of equations only has 2 unknown variables.
I think we can graph those. (Thinking)

For $a=1$ it should look like:
View attachment 5105

 

[evinda]

Shouldn't that be $\left( \frac{a-\frac{3}{2}}{a-\frac{1}{2}}, \frac{2}{a-\frac{1}{2}}, \frac{6a-5}{2a-1}\right)$? (Wondering)

I will remake the operations...

If so, when do we get a degenerate case exactly? (Wondering)

We would get a degenerate solution only if $6a-5=0 \Rightarrow 6a=5 \Rightarrow a= \frac{5}{6}$.
But in this case we have $a> \frac{3}{2}=\frac{9}{6}$. So the above equality is never satisfied.

So now it remains to check the case where we put $P_4$ in the basis? (Thinking)

- - - Updated - - -

The original set of equations only has 2 unknown variables.
I think we can graph those. (Thinking)

For $a=1$ it should look like:

So at this graph do we see that the set of feasible solutions is the blue triangle? (Thinking)

 

[I like Serena]

We would get a degenerate solution only if $6a-5=0 \Rightarrow 6a=5 \Rightarrow a= \frac{5}{6}$.
But in this case we have $a> \frac{3}{2}=\frac{9}{6}$. So the above equality is never satisfied.

So now it remains to check the case where we put $P_4$ in the basis? (Thinking)

Yep. (Nod)

So at this graph do we see that the set of feasible solutions is the blue triangle? (Thinking)

Yes.
In particular we have 3 boundary conditions (lines) in the basic feasible solution $(x_1, x_2) = (0,2)$.
That is for respectively $x_1+2x_2\le 4$, $2x_1+x_2 \le 2$, and $x_1 \ge 0$.
It corresponds to a degenerate basic feasible solution.
It means that when we execute the simplex algorithm that we won't be able to tell in which direction we should go, and we might even get stuck in a cycle. (Nerd)

 

[evinda]

Yep. (Nod)

I chose $P_4$ to get in the basis and I got the following tableau:

$\begin{matrix}
B & b & P_1 & P_2 & P_3 & P_4 & P_5 & \theta & \\
P_3 & 4 & 1 & 1 & 1 & 0 & 0 & & L_1'=L_1+ \frac{1}{2}L_2'\\
P_4 & 2 & 2 & 1 & 0 & 1 & 0 & & L_2'=2L_2\\
P_5 & 3 & 1 & a & 0 & 0 & 1 & & L_3'=L_3+\frac{1}{2}L_2'
\end{matrix}$

Is it right? If so, then we get the same basic feasible non-degenerate solution as the initial one and this means that at this point the algorithm terminates. Right?

So for $a> \frac{3}{2}$ we cannot find a degenerate basic feasible solution. Or am I wrong? (Thinking)

Yes.
In particular we have 3 boundary conditions (lines) in the basic feasible solution $(x_1, x_2) = (0,2)$.
That is for respectively $x_1+2x_2\le 4$, $2x_1+x_2 \le 2$, and $x_1 \ge 0$.
It corresponds to a degenerate basic feasible solution.
It means that when we execute the simplex algorithm that we won't be able to tell in which direction we should go, and we might even get stuck in a cycle. (Nerd)

So you mean that we take into consideration just the first two inequalities? (Thinking)

 

[I like Serena]

Is it right? If so, then we get the same basic feasible non-degenerate solution as the initial one and this means that at this point the algorithm terminates. Right?

There is another basic feasible solution with the basis $P_1, P_3, P_5$ that I haven't seen yet.
Did we miss it? (Wondering)

So for $a> \frac{3}{2}$ we cannot find a degenerate basic feasible solution. Or am I wrong? (Thinking)

That is correct.

So you mean that we take into consideration just the first two inequalities? (Thinking)

We only need to take the inequalities that touch the feasible region into account.
In this case (with $a < \frac 32$) those are the first two inequalities and the non-negativity inequalities.
The 3rd inequality does not touch the feasible region, so we can ignore it. (Nerd)

 

[evinda]

There is another basic feasible solution with the basis $P_1, P_3, P_5$ that I haven't seen yet.
Did we miss it? (Wondering)

Which tableau should we use to get it? (Sweating)

We only need to take the inequalities that touch the feasible region into account.
In this case (with $a < \frac 32$) those are the first two inequalities and the non-negativity inequalities.
The 3rd inequality does not touch the feasible region, so we can ignore it. (Nerd)

In general, the set of feasible solutions is the set where all the inequalities hold.
Why can we ignore the third inequality in this case? Could you explain it further to me? (Thinking)

 

[I like Serena]

Which tableau should we use to get it? (Sweating)

Oh wait, we did already get it: (Wait)

If we start with $P_1$, independently of $a$, we get the following tableau:
$\begin{matrix}
B & b & P_1 & P_2 & P_3 & P_4 & P_5 & \theta & \\
P_3 & 3 & 0 & \frac{1}{2} & 1 & -\frac{1}{2} & 0 & & L_1'=L_1-L_2'\\ \\
P_1 & 1 & 1 & \frac{1}{2} & 0 & \frac{1}{2} & 0 & & L_2'=L_2-L_1'\\ \\
P_5 & 2 & 0 & a-\frac{1}{2} &0 & -\frac{1}{2} & 1 & & L_3'=L_3-aL_1'
\end{matrix}$

In general, the set of feasible solutions is the set where all the inequalities hold.
Why can we ignore the third inequality in this case? Could you explain it further to me? (Thinking)

The blue triangle represents the feasible region.
In that region the third constraint ($x_1 + ax_2 \le 3$) is always satisfied if $a < \frac 32$, so we can leave it out. (Nerd)

 

[evinda]

The blue triangle represents the feasible region.
In that region the third constraint ($x_1 + ax_2 \le 3$) is always satisfied if $a < \frac 32$, so we can leave it out. (Nerd)

How do we deduce that the third constraint ($x_1 + ax_2 \le 3$) is always satisfied if $a < \frac 32$ ?

We have $x_1+ a x_2< x_1+ \frac{3}{2} x_2 \leq x_1+2 x_2 \leq 4$

How can we get that $x_1+ a x_2 \leq 3$ ? (Thinking)

 

[I like Serena]

How do we deduce that the third constraint ($x_1 + ax_2 \le 3$) is always satisfied if $a < \frac 32$ ?

We have $x_1+ a x_2< x_1+ \frac{3}{2} x_2 \leq x_1+2 x_2 \leq 4$

How can we get that $x_1+ a x_2 \leq 3$ ? (Thinking)

By looking at the graph? (Wondering)
The blue triangle is strictly below the green line everywhere (in the first quadrant). (Nerd)

 

[evinda]

Not quite.
We need to walk through all possible basic feasible solutions.
Can't we choose another variable to get in the basis? (Wondering)

Don't we also have to check the case where we have the following tableau:

$\begin{matrix}
B & b & P_1 & P_2 & P_3 & P_4 & P_5 & \theta & \\
P_3 & 4-\frac{6}{a} & 1-\frac{2}{a} & 0 & 1 & 0 & -\frac{2}{a} & & L_1'=L_1-2L_3'\\ \\
P_4 & 2-\frac{3}{a} & 2-\frac{1}{a} & 0 & 0 & 1 & -\frac{1}{a} & & L_2'=L_2-L_3'\\ \\
P_2 & \frac{3}{a} & \frac{1}{a} & 1 & 0 & 0 & \frac{1}{a} & & L_3'=\frac{L_3}{a}
\end{matrix}$

where $a> \frac{3}{2}$

and we choose $P_1$ to get in the basis instead of $P_5$ ?

 

[I like Serena]

Don't we also have to check the case where we have the following tableau:

$\begin{matrix}
B & b & P_1 & P_2 & P_3 & P_4 & P_5 & \theta & \\
P_3 & 4-\frac{6}{a} & 1-\frac{2}{a} & 0 & 1 & 0 & -\frac{2}{a} & & L_1'=L_1-2L_3'\\ \\
P_4 & 2-\frac{3}{a} & 2-\frac{1}{a} & 0 & 0 & 1 & -\frac{1}{a} & & L_2'=L_2-L_3'\\ \\
P_2 & \frac{3}{a} & \frac{1}{a} & 1 & 0 & 0 & \frac{1}{a} & & L_3'=\frac{L_3}{a}
\end{matrix}$

where $a> \frac{3}{2}$

and we choose $P_1$ to get in the basis instead of $P_5$ ?

Ah, did we miss that one?
Yes, we should also check that one. (Nod)

The corresponding graph is:
View attachment 5111
The tableau corresponds to the intersection of the green line with the y-axis.
If we bring in $P_1$ and leave $P_3$, we move to the intersection of the blue line with the green line. (Nerd)
Hmm... didn't we already do that? (Wondering)

 

[evinda]

Ah, did we miss that one?
Yes, we should also check that one. (Nod)

Then we get the following tableau, right?
$\begin{matrix}
B & b & P_1 & P_2 & P_3 & P_4 & P_5 & & \theta & \\
P_3 & \frac{6a-9}{2a-1} & 0 & 0 & 1 & \frac{2-a}{2a-1} & \frac{3}{1-2a} & & &L_1''=L_1'-\left( 1-\frac{2}{a} \right )L_2'' \\ \\
P_1 & \frac{2-\frac{3}{a}}{2-\frac{1}{a}} & 1 & 0 & 0 & \frac{1}{2-\frac{1}{a}} & \frac{1}{1-2a} & & & L_2''=\frac{L_2'}{2-\frac{1}{a}}\\ \\
P_2 & \frac{4}{2a-1} & 0 & 1 & 0 & \frac{1}{1-2a} & \frac{2}{2a-1} & & &L_3''=L_3'-\frac{1}{a}L_2''
\end{matrix}$

This gives a non-degenerate basic feasible solution so we have to continue the algorithm. Right? (Thinking)

Hmm... didn't we already do that? (Wondering)

Did we? At which point? (Thinking)

 

[I like Serena]

Then we get the following tableau, right?
$\begin{matrix}
B & b & P_1 & P_2 & P_3 & P_4 & P_5 & & \theta & \\
P_3 & \frac{6a-9}{2a-1} & 0 & 0 & 1 & \frac{2-a}{2a-1} & \frac{3}{1-2a} & & &L_1''=L_1'-\left( 1-\frac{2}{a} \right )L_2'' \\ \\
P_1 & \frac{2-\frac{3}{a}}{2-\frac{1}{a}} & 1 & 0 & 0 & \frac{1}{2-\frac{1}{a}} & \frac{1}{1-2a} & & & L_2''=\frac{L_2'}{2-\frac{1}{a}}\\ \\
P_2 & \frac{4}{2a-1} & 0 & 1 & 0 & \frac{1}{1-2a} & \frac{2}{2a-1} & & &L_3''=L_3'-\frac{1}{a}L_2''
\end{matrix}$

This gives a non-degenerate basic feasible solution so we have to continue the algorithm. Right? (Thinking)

I don't think that is a feasible solution for $a > \frac 32$.
Instead I think we should move to the basis $P_1, P_2, P_4$. (Thinking)

Did we? At which point? (Thinking)

Turns out we covered basis $P_2, P_3, P_4$ in post #7.
But I can't find basis $P_1, P_2, P_4$. (Nerd)

 

[evinda]

I don't think that is a feasible solution for $a > \frac 32$.

Why isn't it feasible? Aren't all the components positive? (Thinking)

$a> \frac{3}{2} \Rightarrow 2a>3 \Rightarrow 6a>9$

$2a>3 \Rightarrow 2a>1$

$\frac{2-\frac{3}{a}}{2-\frac{1}{a}}=\frac{2a-3}{2a-1}>0$

 

[I like Serena]

Why isn't it feasible? Aren't all the components positive? (Thinking)

$a> \frac{3}{2} \Rightarrow 2a>3 \Rightarrow 6a>9$

$2a>3 \Rightarrow 2a>1$

$\frac{2-\frac{3}{a}}{2-\frac{1}{a}}=\frac{2a-3}{2a-1}>0$

It shouldn't be feasible since it corresponds to the intersection of the red line (non-basic variable $P_4$) and the green line (non-basic variable $P_5$).
https://www.physicsforums.com/attachments/5111
When $a > \frac 32$ that intersection should have either $x_2 < 0$ or $x_1 < 0$.