Finding a general formula for the nth derivative of a partial fraction

[Bolter]

Moved from technical math section, so missing the homework template
Summary:: Find a general formula for the nth derivative

Hi everyone!

How would I approach and answer a Q such as this

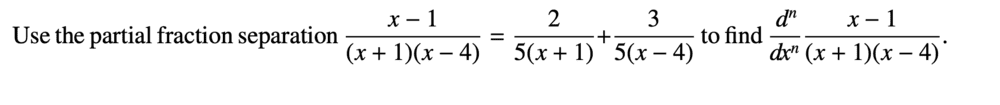
I began by rewriting the expression in a different form, then used chain rule to each given term

I tried to work out the 1st, 2nd and 3rd derivative in order to help me spot a pattern, so that it would help me find a general formula for the nth derivative. But I can't seem to notice too much.

The only thing I see is that signs alternate as you differentiate again and again, and that it has a common factor of 1/5 to take out

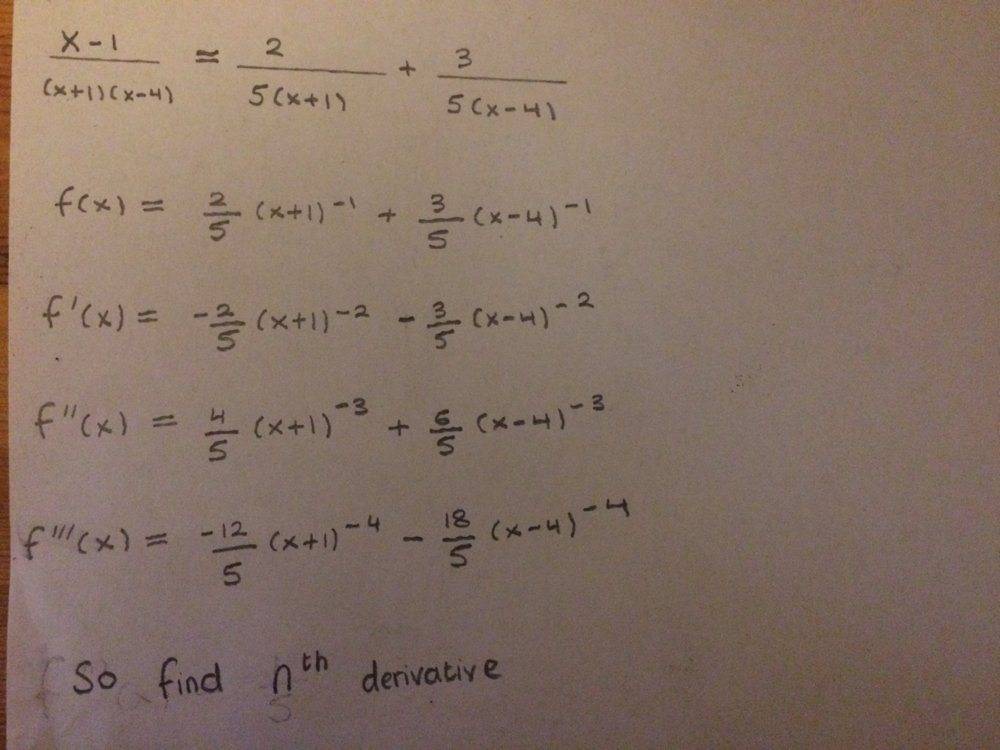
Any help would be appreciated, thanks!

 

[BvU]

If we take the 5 for granted (put it in front of brackets $\ {1\over 5}(...)\$ ) you have a generalization of the form $${d^n\over dx^n}= {1\over 5}\Bigl (\;A (x+1)^p + B (x-4)^q \;\Bigr ) $$ and you have to find A, B, p and q. Not so difficult, especially p and q

 

[Bolter]

If we take the 5 for granted (put it in front of brackets $\ {1\over 5}(...)\$ ) you have a generalization of the form $${d^n\over dx^n}= {1\over 5}\Bigl (\;A (x+1)^p + B (x-4)^q \;\Bigr ) $$ and you have to find A, B, p and q. Not so difficult, especially p and q

Ok so I have come up with this now, following up from what you have shown

I have multiplied my nth derivative my (-1)^n also, to account for the alternating sign changes
My p and q values must be -(n+1) from inspection

Although I still cannot what A and B values must be?
The only pattern that I can see now is that A & B get doubled then tripled then quadrupled then quintuple etc etc each time you differentiate the expression more and more

Does this involve something to do with factorials or I'm I mistaken here?

 

[BvU]

You are not mistaken !

 

[Bolter]

You are not mistaken !

Ok yes, so I have used that in my nth derivative and got this

You can probably see that I redone the differentiation for first, second and third derivative, but this time I did not simplify the coefficients and this is what helped me realized that I had to use the factorial notation

I hope that is right nth derivative formula

 

[PeroK]

Ok yes, so I have used that in my nth derivative and got this

View attachment 255915
You can probably see that I redone the differentiation for first, second and third derivative, but this time I did not simplify the coefficients and this is what helped me realized that I had to use the factorial notation

I hope that is right nth derivative formula

One way to check the formula you have found is to use induction.

 

[Bolter]

One way to check the formula you have found is to use induction.

I would but I haven't come across to using induction yet

 

[PeroK]

I would but I haven't come across to using induction yet

There are two steps:

1) Show that your equation holds for n = 1 (possibly $n=0$ as well).

2) Show that if your equation holds for $n = k$ then it holds for $n = k+1$.

Then you are done!

 

[Bolter]

There are two steps:

1) Show that your equation holds for n = 1 (possibly $n=0$ as well).

2) Show that if your equation holds for $n = k$ then it holds for $n = k+1$.

Then you are done!

Ahh so it's essentially a proof method then

I had given that a go and I do see that when n=1, it does give back the first order derivative that I found from before

 

[PeroK]

Okay, so if you differentiate that, do you get your formula for $n = k+1$?