mathmari
Gold Member
MHB
- 4,984
- 7
Hey! 
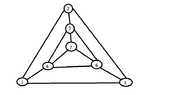
We have the following graph:
View attachment 5841 I want to find a minimal vertex cover.
I thought that the set $C^\star=\{4,5,6\}$ is a minimal vertx cover. Is this correct? How could we prove it? (Wondering) Then I want to find a vertex cover using the following approximation algorithm
I have done the following:
Suppose we start with e=(1,4) then C={1,4} and the graph is the following:
View attachment 5842
Then when we choose e=(5,7) we have C={1,4,5,7} and the graph will look as follows:
View attachment 5843
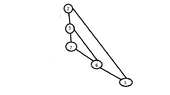
Then we can choose e=(2,3) and then we have C={1,2,3,4,5,7} and the graph will be:
View attachment 5844
Have we finished now?
Is a minimal vertex cover the set $C=\{1,2,3,4,5,7\}$ ? (Wondering)
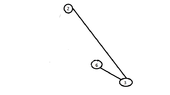
Suppose we start with e=(4,5) then C={4,5} and the graph is the following:
View attachment 5845
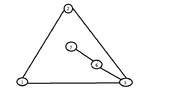
Then when we choose e=(3,6) we have C={3,4,5,6} and the graph will look as follows:
View attachment 5846
Then we choose e=(1,2) and then we have C={1,2,3,4,5,6} and the graph will be:
View attachment 5847
So, a minimal vertex cover is the set $C=\{1,2,3,4,5,6\}$, right? (Wondering)
Does this mean that no matter which edge we choose at each step the minimal vertex cover will contain $6$ vertices? (Wondering) After that I want to find a maximal independent set of vertices and a maximal clique. Could you give me some hints how we could find them? (Wondering)
We have the following graph:
View attachment 5841 I want to find a minimal vertex cover.
I thought that the set $C^\star=\{4,5,6\}$ is a minimal vertx cover. Is this correct? How could we prove it? (Wondering) Then I want to find a vertex cover using the following approximation algorithm
Code:
C <- 0
while E ≠ 0 do
choose e = (u,v) ∈ E arbitrary
C <- C U {u,v}
G <- G - {u,v}
return CI have done the following:
Suppose we start with e=(1,4) then C={1,4} and the graph is the following:
View attachment 5842
Then when we choose e=(5,7) we have C={1,4,5,7} and the graph will look as follows:
View attachment 5843
Then we can choose e=(2,3) and then we have C={1,2,3,4,5,7} and the graph will be:
View attachment 5844
Have we finished now?
Is a minimal vertex cover the set $C=\{1,2,3,4,5,7\}$ ? (Wondering)
Suppose we start with e=(4,5) then C={4,5} and the graph is the following:
View attachment 5845
Then when we choose e=(3,6) we have C={3,4,5,6} and the graph will look as follows:
View attachment 5846
Then we choose e=(1,2) and then we have C={1,2,3,4,5,6} and the graph will be:
View attachment 5847
So, a minimal vertex cover is the set $C=\{1,2,3,4,5,6\}$, right? (Wondering)
Does this mean that no matter which edge we choose at each step the minimal vertex cover will contain $6$ vertices? (Wondering) After that I want to find a maximal independent set of vertices and a maximal clique. Could you give me some hints how we could find them? (Wondering)