Finding acceleration of block connected to pulley with mass

[AdityaDev]

Homework Statement

Homework Equations

a=Rα

The Attempt at a Solution

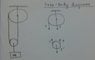
Free body diagrams:

For larger pulley, TR=Iα ⇒ T=½MRα
If this pulley rotates by some amount suchat x length of rope becomes free, and if I hold the smaller pulley at rest, then this extra length of rope comes bellow the pulley. So the small pulley can go down by x/2 distance.
Hence for every θ rotation, the small pulley goes down by Rθ/2.
For smaller pulley, T'-2T+Mg/2=Ma/2 and for block, T'=Ma+Mg
So ssubstituting T', 2T-Ma/2=3Mg/2
Now if rope comes down at a rate of Rα, then pulley goes down by Rα/2
Hence a=Rα/2
After plugging in all values, I am not getting the answer.

 

[Chestermiller]

Please re-check your force balance on the block.

Chet

 

[AdityaDev]

Please re-check your force balance on the block.

Chet

Its Mg-T'=Ma so T'=Mg-Ma
T'-2T+Mg/2=Ma/2
Substituting...
3Mg/2-2T=3Ma/2
So 3Mg/2=¾MRα+MRα=7/4 (MRα)

 

[Chestermiller]

So does this give the "correct answer" now?

Chet

 

[AdityaDev]

It doesnt. Its given that the acceleration of block is 2g/5.

 

[Chestermiller]

It doesnt. Its given that the acceleration of block is 2g/5.

OK. Here are a couple of things to think about:

1. The angular acceleration of the upper pulley is not equal to the acceleration of the block divided by R. Kinematically, the tangential velocity of the upper pulley is twice the downward velocity of the block.

2. The two tensions, which you call T, are not equal. There has to be a tension difference in order to rotationally accelerate the lower pulley. You need to do a moment balance on the lower pulley.

Chet

 

[AdityaDev]

OK. Here are a couple of things to think about:

1. The angular acceleration of the upper pulley is not equal to the acceleration of the block divided by R. Kinematically, the tangential velocity of the upper pulley is twice the downward velocity of the block.

I already proved this in post 1.
can there be two different tensions on a single massless string?

 

[Chestermiller]

I already proved this in post 1.
can there be two different tensions on a single massless string?

Yes, if it is turning a pulley with mass, and does not slip.

 

[AdityaDev]

How? If yes, then does the tension change uniformly? If a segment of massless string has two different forces on either end, then it will have a non zero acceleration.

 

[Chestermiller]

How? If yes, then does the tension change uniformly? If a segment of massless string has two different forces on either end, then it will have a non zero acceleration.

There is a distributed tangential static frictional force exerted on the string by the pulley over its contact length with the pulley.

Chet

 

[AdityaDev]

I am not able to find a relation between the three tensions.

 

[Chestermiller]

I am not able to find a relation between the three tensions.

OK. You are basically dealing with 4 linear algebraic equations in 4 unknowns.

Unknowns:
1. Tension in the part of the upper rope to the left of the lower pulley T_L
2. Tension in the part of the upper rope to the right of the lower pulley T_R
3. Tension in the lower rope T'
4. Acceleration of the block a

Equations:
1. Moment balance on upper pulley
2. Moment balance on lower pulley
3. Force balance on lower pulley
4. Force balance on block

In my judgement, the complicated part of this problem is not in setting up the force and moment balances. It is in establishing the kinematics. Please summarize for me again, in terms of the acceleration of the lower pulley a, what you got for

1. The angular acceleration of the upper pulley α_U
2. The angular acceleration of the lower pulley α_L

Chet

 

[AdityaDev]

New equations:

1)torque equation for large pulley
$T_1=1/2MR\alpha$

2)torque equations for small pulley
$(T_2-T_1)R/2=\frac{1}{2}\frac{M}{2}\frac{R^2}{4}\alpha_1$
$T_2-T_1=\frac{MR^2\alpha_1}{8}$

3)Force equation for block
$Mg-T_3=Ma_1$

4)Force equation for small pulley
$T_3-T_1-T_2+Mg/2=Ma_1/2$

5)Relation connecting $\alpha_1$ and $\alpha_2$
If Rθ string comes out, then the pulley moves down by Rθ/2.
And i know that if lower pulley rotates by 2π, it moves a distance of 2πR/2 since radius is R/2.
To move a distance of Rθ/2, the pulley has to rotate by $\frac{2\pi}{\pi R}.R\theta/2=\theta$
So if upper pulley rotates by θ, then the lower pulley also rotates by θ?

 

[Chestermiller]

Yes. Everything is correct.

So, in your notation, $α=α_1=\frac{2a_1}{R}$

Chet

 

[AdityaDev]

Now $T_1=1/2MR\alpha$
$T_2=T_1+1/8MR\alpha=(5/8)MR\alpha$
$T_3=Mg-(1/2)MR\alpha$
Now $Mg-(1/2)MR\alpha-1/2MR\alpha-(5/8)MR\alpha+Mg/2=(1/4)MR\alpha$
Got the answer. Thank you for helping.