Finding acceleration of cylinder

[Saitama]

Homework Statement

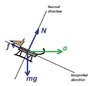
(see attachment)

Homework Equations

The Attempt at a Solution

Can I use the instantaneous axis of rotation for this question?

I placed it at the point of contact of cylinder and the ground. Moment of inertia about it is: $4mR^2/2+4mR^2+mx^2=6mR^2+mx^2$, where m is the mass of dog and x is the distance of it from the axis. x can be calculated using the cosine rule i.e
$$\cos(150^o)=\frac{R^2+R^2-x^2}{2R^2} \Rightarrow \frac{x^2}{2R^2}=1+\frac{\sqrt{3}}{2} \Rightarrow x=\sqrt{2+\sqrt{3}}R$$

Toque about the axis is $mgx\sin(15^o)=I\alpha=Ia/R$. Substituting the values of x and I, I don't get the right answer.

Any help is appreciated. Thanks!

 

[TSny]

Only the cylinder rotates about the point of contact, the dog is moving along a horizontal line. So, when you set up $\tau = dL/dt$ about the point of contact, you might want to separate out the contributions of the cylinder and dog to $L$. So,

$\tau = dL_{cyl}/dt + dL_{dog}/dt$

 

[Saitama]

Only the cylinder rotates about the point of contact, the dog is moving along a horizontal line. So, when you set up $\tau = dL/dt$ about the point of contact, you might want to separate out the contributions of the cylinder and dog to $L$. So,

$\tau = dL_{cyl}/dt + dL_{dog}/dt$

Does that mean it is fine to use the instantaneous axis of rotation?

$$L_{cyl}=6mR^2\omega=6mRv$$
$$L_{dog}=mxv$$
Are these correct?

 

[TSny]

The expression for $L_{dog}$ is not quite correct. Recall, for a particle $L = rpsin\phi = r_{\bot} p$ where $r_{\bot}$ is "moment arm" for p.

 

[Saitama]

The expression for $L_{dog}$ is not quite correct. Recall, for a particle $L = rpsin\phi = r_{\bot} p$.

Is it $mxv\sin(15^o)$?

 

[TSny]

No, did you use the correct trig function here? $r_{\bot}$ is the perpendicular distance from the point of contact to the line of motion of the dog.

 

[Saitama]

No, did you use the correct trig function here? $r_{\bot}$ is the perpendicular distance from the point of contact to the line of motion of the dog.

Oh yes, sorry about that. As the dog moves horizontally, r_{\bot} is $x\cos(15^o)$, so $L_{dog}=mxv\cos(15^o)$.

Differentiating the expression for $L_{cyl}$ and $L_{dog}$ w.r.t time
$$\frac{dL_{cyl}}{dt}=6mRa$$
$$\frac{dL_{dog}}{dt}=mxa\cos(15^o)$$
Hence,
$$\tau=I\alpha=6mRa+mxa\cos(15^o)$$
Should I plug in the values of I and x from my first post?

 

[TSny]

Looks like you left out the cos(15) in mxa. [EDIT: I see you already fixed that.] Yes, you can plug in your value of x. But, you might just want to write $r_{\bot}$ directly in terms of R and the angle of 30 degrees. I think it will be a little nicer. But it should all come out the same in the end.

 

[Saitama]

Looks like you left out the cos(15) in mxa. [EDIT: I see you already fixed that.] Yes, you can plug in your value of x. But, you might just want to write $r_{\bot}$ directly in terms of R and the angle of 30 degrees. I think it will be a little nicer. But it should all come out the same in the end.

I edited my previous post. :)

But the $a$ cancels out in my torque equation.

 

[TSny]

I thought you were using mgxsin(15) for the torque? xsin(15) can be written in a nice way in terms of R and the 30 degrees.

 

[Saitama]

I thought you were using mgxsin(15) for the torque? xsin(15) can be written in a nice way in terms of R and the 30 degrees.

This may be a dumb question but why can't I use $I\alpha$?

And I can use a calculator to evaluate sin(15) so I don't need to worry about expressing it in terms of 30 degrees. :)

 

[TSny]

This may be a dumb question but why can't I use $I\alpha$?

The general law is $\tau = dL_{sys}/dt$. For the cylinder, you can write $dL/dt = I\alpha$ while for the dog you found $dL/dt = mxacos(15)$.

So, you have the right hand side of $\tau = dL/dt$ figured out. You just need to think about what to put in for the torque for the left hand side. And I think you had that figured out in your first post.

And I can use a calculator to evaluate sin(15) so I don't need to worry about expressing it in terms of 30 degrees. :)

Aww.

 

[Saitama]

The general law is $\tau = dL/dt$. For the cylinder, you can write $dL/dt = I\alpha$ while for the dog you found $dL/dt = mxacos(15)$.

So, you have the right hand side of $\tau = dL/dt$ figured out. You just need to think about what to put in for the torque for the left hand side. And I think you had that figured out in your first post.

Thanks TSny, $a$ comes out be 0.6177 m/s^2. Is this right?

Is it possible to do this question by taking torque about the CM of the cylinder? I tried it before switching to the instantaneous axis but I was stuck on the direction of friction. How can I find it?

 

[TSny]

Thanks TSny, $a$ comes out be 0.6177 m/s^2. Is this right?

Pretty close to what I got. Might be some round off error (which can be avoided by writing things in terms of R and 30 degrees and not plugging in numbers until the end. R will cancel out.) See if you can show that the answer can be expressed as

a = gsin30/(7+cos30)

Is it possible to do this question by taking torque about the CM of the cylinder? I tried it before switching to the instantaneous axis but I was stuck on the direction of friction. How can I find it?

The friction force at the ground is the only external force acting on the system horizontally. So, that should tell you the direction of the the friction force from the ground. You need to be careful if you want to take torques about the CM of the cylinder, since the CM of the cylinder is not the same as the CM of the system. However, the CM of the cylinder and the CM of the system have the same acceleration in this problem. So, I think you would be ok in taking torques about the CM of the cylinder.

Of course, you can always treat the cylinder and dog separately. You would then draw free body diagrams for each. For the cylinder, you could take torques about the CM of the cylinder. The algebra is more involved now because you will have to take into account the normal and friction force between the dog and cylinder.

 

[Saitama]

Pretty close to what I got. Might be some round off error (which can be avoided by writing things in terms of R and 30 degrees and not plugging in numbers until the end. R will cancel out.) See if you can show that the answer can be expressed as

a = gsin30/(7+cos30)

I reached that answer. xin(15) is equivalent to Rsin(30) and xcos(15) is equivalent R(1+cos(30)). This was obvious from the diagram. I should have done that before.

Thanks you.

The friction force at the ground is the only external force acting on the system horizontally. So, that should tell you the direction of the the friction force from the ground. You need to be careful if you want to take torques about the CM of the cylinder, since the CM of the cylinder is not the same as the CM of the system. However, the CM of the cylinder and the CM of the system have the same acceleration in this problem. So, I think you would be ok in taking torques about the CM of the cylinder.

Of course, you can always treat the cylinder and dog separately. You would then draw free body diagrams for each. For the cylinder, you could take torques about the CM of the cylinder. The algebra is more involved now because you will have to take into account the normal and friction force between the dog and cylinder.

Okay, so the direction of friction on the cylinder from the ground is in the right direction ($f_1$) and from the dog, its tangential in the direction opposite to the motion of dog ($f_2$).

This will give me 2 equations:
$$f_1=4ma$$
$$f_1R-f_2R=I\alpha$$

Am I doing this right? :)

 

[TSny]

If you're going to treat the cylinder alone, then there will be horizontal components of the normal and friction forces from the the dog that will need to be included in ƩF_x = (4m)a

For the torque equation for cylinder, make sure you have the correct direction for the frictional torque from the dog (due to $f_2$). I'm not sure whether you're taking clockwise or counterclockwise as positive rotational direction. [EDIT: Never mind, I thought you had a + sign rather than a - sign in the torque equation. But, still, it would be nice to know your sign convention for the rotation.]

 

[Saitama]

If you're going to treat the cylinder alone, then there will be horizontal components of the normal and friction forces from the the dog that will need to be included in ƩF_x = (4m)a

For the torque equation for cylinder, make sure you have the correct direction for the frictional torque from the dog (due to $f_2$). I'm not sure whether you're taking clockwise or counterclockwise as positive rotational direction.

I am treating them separately. I will rewrite everything again. Please see my attachment. The direction of forces are shown. I have not shown the normal reaction from the ground on the cylinder. :)

$f_2=mg\sin(30^o)$, $N=mg\cos(30^o)$

$$\sum F_x=f_1+f_2\cos(30^o)-N\sin(30^o)=4ma$$

Is this correct?
I feel that direction of f_2 is incorrect.

 

[TSny]

I am treating them separately. I will rewrite everything again. Please see my attachment. The direction of forces are shown. I have not shown the normal reaction from the ground on the cylinder. :)

Diagram looks good.

$f_2=mg\sin(30^o)$, $N=mg\cos(30^o)$

These equations are not correct. To get the correct equations for f₂ and N, you will need to apply 2nd law to the dog.

$$\sum F_x=f_1+f_2\cos(30^o)-N\sin(30^o)=4ma$$

This looks correct.

I feel that direction of f_2 is incorrect.

I think you have the direction for f₂ on the cylinder correct.

 

[Saitama]

These equations are not correct. To get the correct equations for f₂ and N, you will need to apply 2nd law to the dog.

The forces acting on the dog are friction (f_2), mg and normal reaction from the cylinder
For the tangential motion, $mg\sin(30^o)-f_2=ma$ and for the horizontal motion, $N\cos(60^o)-f_2\cos(30^o)=ma$. Is this correct now?

 

[TSny]

For the tangential motion, $mg\sin(30^o)-f_2=ma$ and for the horizontal motion, $N\cos(60^o)-f_2\cos(30^o)=ma$. Is this correct now?

For the tangential direction, you'll need the component of acceleration in the tangential direction.

Horizontal equation looks good.

 

[Saitama]

For the tangential direction, you'll need the component of acceleration in the tangential direction.

Why? Isn't it a, I mean, the acceleration is $\alpha R$ which is $a$? Or is it $(a+a\cos(30^o))$?

 

[TSny]

Why? Isn't it a, I mean, the acceleration is $\alpha R$ which is $a$? Or is it $(a+a\cos(30^o))$?

What is the direction of the acceleration of the dog?

 

[Saitama]

What is the direction of the acceleration of the dog?

Won't it be resultant of the two accelerations, one in horizontal direction and the other in tangential direction?

 

[TSny]

Won't it be resultant of the two accelerations, one in horizontal direction and the other in tangential direction?

No. You're standing on the ground as this contraption comes by. It's pitch dark except for a small light on Fido's nose and a small light carried by the center of the cylinder. What direction of acceleration do you see for the light on Fido's nose? How does it compare to the acceleration of the center of the cylinder?

 

[Saitama]

No. You're standing on the ground as this contraption comes by. It's pitch dark except for a small light on Fido's nose and a small light carried by the center of the cylinder. What direction of acceleration do you see for the light on Fido's nose? How does it compare to the acceleration of the center of the cylinder?

I still don't get it. The light on Fido's nose performs circular motion about centre of cylinder with a tangential acceleration of a and moves in horizontal direction again with an acceleration of $a$.

If someone sits on the centre of cylinder, he/she would see that Fido's nose moves about the centre in a clockwise manner.

 

[TSny]

You are given that Fido stays at a constant height above the floor. It's like he's on a rolling treadmill that's continually speeding up (poor dog). From the point of view of the CM of the cylinder, the dog remains at rest.

 

[Saitama]

You are given that Fido stays at a constant height above the floor. It's like he's on a rolling treadmill that's continually speeding up (poor dog). From the point of view of the CM of the cylinder, the dog remains at rest.

I am not sure but does that mean I need to consider the tangential acceleration zero and equate the forces in the tangential direction? Sorry if this is getting annoying for you. -.-'

 

[TSny]

I am not sure but does that mean I need to consider the tangential acceleration zero and equate the forces in the tangential direction? Sorry if this is getting annoying for you. -.-'

No problem. I do have to leave for a while.

Try setting up 2nd law for components in the tangential and normal directions. See attachment.
This should allow you to express f and N in terms of the unknown acceleration.

 

[Chestermiller]

There is a much easier way of doing this problem. You first focus on the dog and consider a free body diagram on the dog. The dog is moving horizontally, with an acceleration a. The cylinder is exerting a force on the dog that can be resolved into horizontal and vertical components H and V. The only other force on the dog is gravity. So,
V = mg
H = ma

The dog exerts equal and opposite forces on the cylinder. So the vertical component of the dog force on the cylinder is -V = -mg, and the horizontal force of the dog on the cylinder is -H = -ma. Now a free body diagram can be done on the cylinder. The ground exerts a force on the cylinder that can be resolved into horizontal and vertical components N and F respectively, where N is the normal force, and F is the frictional force (pointing in the direction of the cylinder movement). So the force balances in the horizontal and vertical directions on the cylinder are:

N = Mg + V = (M+m)g
Ma = F - ma

Next, performing a moment balance on the cylinder around its center of mass, we get:

Iα = VRsin30-HRcos30-FR = mgRsin30-maRcos30-(M+m)aR=mgRsin30-(mcos30+M+m)Ra

where α is the clockwise angular acceleration. The angular acceleration in this problem is related kinematically to the linear acceleration a by:

a = αR

If we substitute this into the previous equation, we can solve for the acceleration a:

$$a=\frac{mgR^2sin30}{I+(mcos30+M+m)R^2}$$

For a solid cylinder, the moment of inertia is given by:

$$I=M\frac{R^2}{2}$$

Sutstituting, we get,

$$a=\frac{msin30}{m(1+cos30)+\frac{3M}{2}}g$$

I hope I did the algebra correctly.

Chet

 

[Saitama]

No problem. I do have to leave for a while.

Try setting up 2nd law for components in the tangential and normal directions. See attachment.
This should allow you to express f and N in terms of the unknown acceleration.

For tangential direction: $mg\sin(30^o)-f_2=ma\cos(30^o)$
For normal direction: $N-mg\cos(30^o)=ma\sin(30^o)$

Looks good now? :)

Thank you Chet for the alternative solution, your answer does reduces to the correct answer when you plug in M=4m.