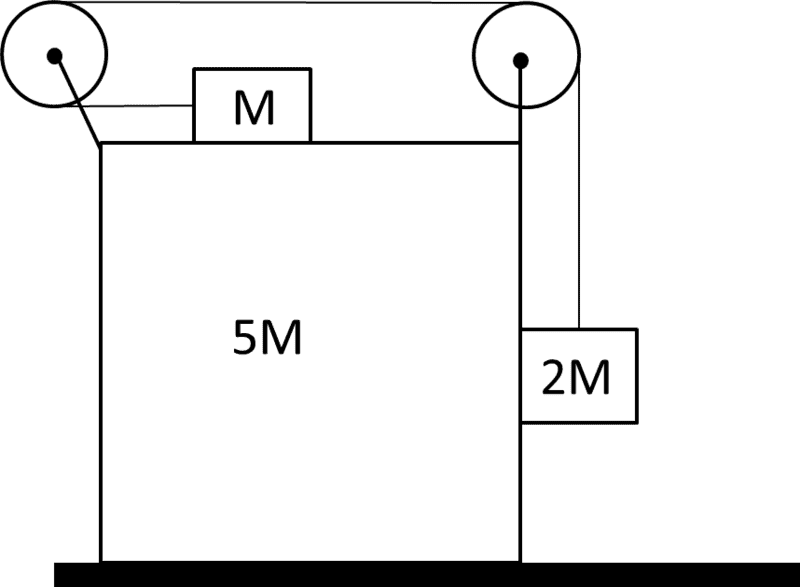
Just to show some more steps:
View attachment 327898The global frame of reference is fixed to the ground, and the FBD's show forces relevant to solving the problem.
Horizontal Direction for Block 1M
$$ T = M( a_1 - a_5) \tag{1}$$
Vertical Direction for Block 2M:
$$ \begin{aligned} 2Mg - T &= 2Ma_2 \\ & \implies T = 2M(g-a_2) \quad\quad \text{(2)} \end{aligned}$$Given a positive acceleration ##a_2## will result in a positive acceleration ##a_1##, hence ##a_2 = a_1##, combine (1) and (2) with the constraint:
$$ \begin{aligned} M( a_1 -a_5) &=2M(g-a_2) \\ &= 2M(g-a_1) \\ & \implies a_1 = \frac{2g+a_5}{3} \quad\quad \text{(3)} \end{aligned}$$
Horizontal Direction of Block 2M:
$$ \begin{aligned} -N &= -2Ma_5 \\ & \implies N = 2Ma_5 \quad\quad \text{(4)} \end{aligned}$$
Horizontal Direction of Block 5M:
$$ \begin{aligned} T -2T + N &= -5Ma_5 \\ -T + N &= -5Ma_5\quad\quad \text{(5)} \end{aligned} $$
Combine (4) and (5) (substituting for N) to yield:
$$T = 7Ma_5 \tag{6}$$
Lastly combine (1) , (3) and (6) to eliminate ##T## and ##a_1##:
$$ \begin{aligned} \cancel{M}(a_1-a_5) = 7\cancel{M}a_5 \\ \frac{2g+a_5}{3} - a_5 = 7a_5 \\ & \implies a5 = \frac{2}{23}g \end{aligned}$$
I initially kept getting the wrong answer until realized that I had assumed a negative acceleration for block 5M in the horizontal force balance for block 1M. As a result, I needed to keep that assumption throughout the analysis (hence the negative signs on the RHS of (4) and (5) become important). Anyhow, thought I would share my trials and tribulations in case others were having the same difficulty there.