Albert1
- 1,221
- 0
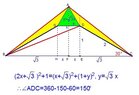
$\triangle ABC, \overline{AB}=\overline {AC}$,there exists an inner point ${D}$ and satisfyng :
(1)$\overline {AB}=\overline {AC}=\overline {BD}$
(2)$\angle DCB=30^o$
find $\angle ADC=?$
(1)$\overline {AB}=\overline {AC}=\overline {BD}$
(2)$\angle DCB=30^o$
find $\angle ADC=?$