MHB Finding Angle at $\gamma$ - Help Requested

  • Thread starter Thread starter Carla1985
  • Start date Start date
  • Tags Tags
    Angle
AI Thread Summary
To determine the angle at $\gamma$, the vertical angles theorem is suggested, but it may not directly apply if $\gamma$ is perceived as part of a circle's edge. The user expresses confusion, indicating that $\gamma$ should represent the angle formed by two intersecting lines rather than a segment of the circle. Clarification is sought on how to accurately calculate this angle. The discussion emphasizes the need for a clear understanding of angle definitions in relation to geometric figures. Overall, the conversation highlights the importance of correctly identifying the components involved in angle measurement.
Carla1985
Messages
91
Reaction score
0
View attachment 6256
Hi,

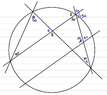
could someone please tell me what theorem I need to be looking at to work out the angle at $\gamma$ please? I've worked out the rest but can't find a theorem for this one.

Thanks
 

Attachments

  • General - 20161101_20115 p.m. - 10.png
    General - 20161101_20115 p.m. - 10.png
    26.7 KB · Views: 84
Mathematics news on Phys.org
Use the vertical angles theorem.
 
Euge said:
Use the vertical angles theorem.

Thanks but that just gives me the angle between the two straight lines. My impression was that $\gamma$ was the part of the angle up to the edge of the circle.
 
That would not make an angle, for an angle is formed by two straight lines. It would only make sense for $gamma$ to be the angle between those two lines.
 
Euge said:
That would not make an angle, for an angle is formed by two straight lines. It would only make sense for $gamma$ to be the angle between those two lines.

That would make things a whole lot easier. Thank you for your help!
 

Thread 'Non-orthogonal bases'

Suppose ,instead of the usual x,y coordinate system with an I basis vector along the x -axis and a corresponding j basis vector along the y-axis we instead have a different pair of basis vectors ,call them e and f along their respective axes. I have seen that this is an important subject in maths My question is what physical applications does such a model apply to? I am asking here because I have devoted quite a lot of time in the past to understanding convectors and the dual...
View full post »

Thread 'What Exactly is Dirac’s Delta Function? - Insight'

Insights auto threads is broken atm, so I'm manually creating these for new Insight articles. In Dirac’s Principles of Quantum Mechanics published in 1930 he introduced a “convenient notation” he referred to as a “delta function” which he treated as a continuum analog to the discrete Kronecker delta. The Kronecker delta is simply the indexed components of the identity operator in matrix algebra Source: https://www.physicsforums.com/insights/what-exactly-is-diracs-delta-function/ by...
View full post »

Similar threads

MHB Can You Find the Angle in This Isosceles Triangle Problem?
Replies
1
Views
1K
B How to draw a plane intersecting a cylinder at a "compound angle"
Replies
8
Views
3K
I Help with area formula using direction cosines
Replies
3
Views
2K
MHB Solve for the angles in a triangle
Replies
4
Views
2K
B Compound Angle Formula: Solving Double Angle Equations
Replies
5
Views
1K
B Angle of the diagonal of a cube
Replies
21
Views
4K
MHB How do I calculate the side of a rhombus using the bisector of an angle theorem?
Replies
1
Views
2K
MHB Can an Ellipse Help Solve the Scalene Triangle Problem?
Replies
1
Views
1K
MHB Proving the Angle-Angle-Side Theorem
Replies
1
Views
2K
MHB Find Angles of Spherical Triangle $\mathcal{P}$
Replies
1
Views
2K

Hot Threads

Recent Insights

Back
Top