Finding Angle P in Isosceles Triangle $PQR$

[anemone]

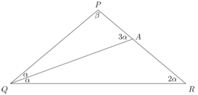
Triangle $PQR$ is an isosceles triangle with $PQ=PR$. Given that the angle bisector at $Q$ meets $PR$ at $A$ and that $QR=QA+PA$. Find angle $P$.

 

[Opalg]

[sp]

View attachment 2415​

With the angles labelled as in the diagram, $\beta = \pi - 4\alpha.$

By the sine rule in triangle $QAP$, $$ \frac{QA}{\sin4\alpha} = \frac{PA}{\sin\alpha} = \frac{QP}{\sin3\alpha}.$$ Therefore $$QA = \frac{\sin4\alpha}{\sin3\alpha}QP, \qquad PA = \frac{\sin\alpha}{\sin3\alpha}QP.$$ By the sine rule in triangle $PQR$, $\dfrac{QR}{\sin4\alpha} = \dfrac{QP}{\sin2\alpha}$ and therefore $QR = \dfrac{\sin4\alpha}{\sin2\alpha}QP = 2\cos2\alpha\cdot QP.$ But $QR = QA + PA$ and so $$\frac{\sin4\alpha}{\sin3\alpha} + \frac{\sin\alpha}{\sin3\alpha} = 2\cos2\alpha,$$ $$\sin4\alpha + \sin\alpha = 2\cos2\alpha\sin3\alpha = \sin5\alpha + \sin\alpha$$ (using the addition formula $2\sin x \cos y = \sin(x+y) + \sin(x-y)$). Therefore $\sin4\alpha = \sin5\alpha$, which means that $4\alpha = \pi - 5\alpha$, or $\alpha = \pi/9$. Finally, $\beta = \pi - 4\alpha = 5\pi/9$, or in degrees $\beta = 100^\circ.$[/sp]

 

[anemone]

Thanks for participating and your elegant solution, Opalg!:)