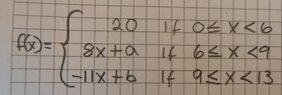Finding Constants for a Piecewise Defined Function

[Mille89]

hi(Smile)
I need some start help finding the two constants a and b:

Do i start like this?:
\(\displaystyle \lim_{{x}\to{6-}} (20) = \lim_{{x}\to{6+}} (8x+a)\)View attachment 8782

 

[Evgeny.Makarov]

Hi, and welcome to the forum.

Do i start like this?:
\lim_{{x}\to{6-}} (20) = \lim_{{x}\to{6+}} (8x+a)

If you need the function to be continuous, then yes.

You can typeset your formulas by enclosing them in [MATH]...[/MATH] tags (button with $\sum$ on the toolbar) or dollar signs.

 

[Mille89]

Hi, and welcome to the forum.

If you need the function to be continuous, then yes.

You can typeset your formulas by enclosing them in [MATH]...[/MATH] tags (button with $\sum$ on the toolbar) or dollar signs.

Thank you(Smile)(Yes)