- #1
rockerman
- 14
- 0
Given two quadratics of the form $f(x) = x'Q_1x$ and $g(x) = x'Q_2x$ and assuming $Q_1$ and $Q_2$ are negative definite matrices, how can I find the lines that are formed by their crossing? here I'm assuming $x \in \mathbb{R}^2$.
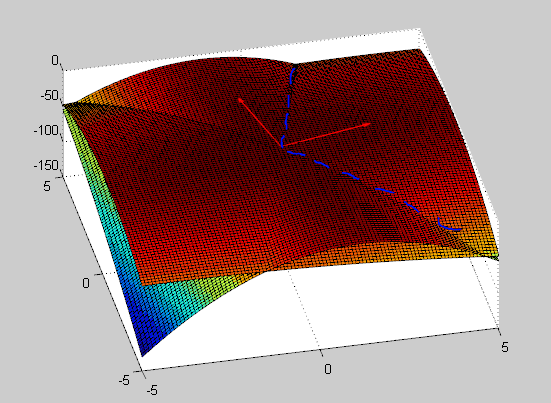

I'm interested in finding vectors $w_1$ and $w_2$ that are parallel to the blue dashed line. I also outlined the eigenvectors of $Q_1-Q-2$, they seem to point exact in the middle of each region.
I'm interested in finding vectors $w_1$ and $w_2$ that are parallel to the blue dashed line. I also outlined the eigenvectors of $Q_1-Q-2$, they seem to point exact in the middle of each region.