- #1
LeitHunt
Homework Statement
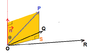
Find th distance of point P to the plane OQR, O being the origin.
"PS" is perpendicular to plane "OQR"
P(3,-2,-1)
S(x,y,z)
O(0,0,0)
Q(1,3,4)
R(2,1,-2)
Homework Equations
A) The equation in terms of (x,y,z) obtain by triple product of OS,OQ & OR.
OS.(OQXOR)=0... [all being co-planar therefore =0]
we get,
-10x+10y-5z=0
B)The Equation on which I'm stuck.I didn't get how PS vector is obtained from coordinates of P & S ;PS=(3-x)i+(-2-y)j+(-1-z)k
Then direction ratio is used to get
x+y=1
y+2z=-4
Now we have 3 equations & 3 Unknowns
The Attempt at a Solution
I understood how first equation is obtained that means by using theorem :- three vector being co-planar then
A.(BXC)=0... (as we get volume from this, being co-planar means no volume)
So equation 1 is obtained that way
Now in Second equation
Vector cross product is done OQ X OR= -10i + 10j -5k
Then,
Where I'm stuck:-
Vector PS is given by (3-X)i + (-2-Y)j+(-1-Z)k,
How? Vector PS is obtained by coordinate of P & S?
Next two equations are simple it just uses the direction ratio.
Solving 3 equation I'll get x,y& z.
Then find vector PS from above and find magnitude of PS that means it's length.
For reference please check below image :-
https://m.imgur.com/a/dEXAT