Finding eigenvalues and eigenvectors given sub-matrices

[member 731016]

Homework Statement

Please see below

Relevant Equations

Please see below

For this,

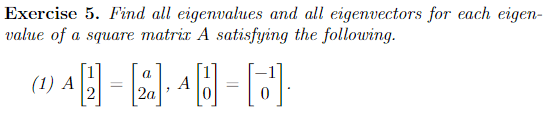
The solution is,

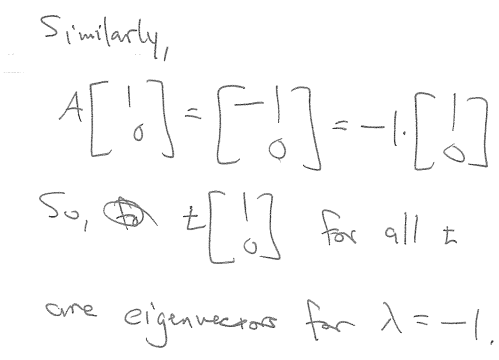
However, does someone please know what allows them to express the eigenvector for each of the sub-matrix in terms of t?

Many thanks!

 

[hutchphd]

From the definition a multiple of any eigenvector is also trivially an eigenvector. So who did this?

 

[FactChecker]

Any matrix operator is linear. So $A (tv)= t A v$ for any vector, $v$.
Now use that in your case with the eigenvector and eigenvalue.

 

[martinbn]

You need to take into account that both conditions hold. If $a\not = -1$, then there are two eigenvalues and the corresponding eigenvectors are multiples of the two given vectors. If $a=-1$, then there is only one eigenvalue and all vectors are eigenvectors.

 

[member 731016]

Thank you for your replies @hutchphd, @FactChecker and @martinbn !

So I am coming to think of it like this considering the most general case I could think of:

$A\vec v = \lambda\vec v$
$At\vec v = \lambda t\vec v$ multiply both sides by a scalar $t$ which is a member of the reals
Therefore, the definition of eigenvector and eigenvalue, $t\vec v$ is an eigenvectors for $\lambda$ and $\lambda$ is the eigenvalue for A.

Is that please correct?

Many thanks!

 

[FactChecker]

$A\vec v = \lambda\vec v$
$At\vec v = \lambda t\vec v$ multiply both sides by a scalar $t$ which is a member of the reals
Therefore, the definition of eigenvector and eigenvalue, $t\vec v$ is an eigenvectors for $\lambda$ and $\lambda$ is the eigenvalue for A.

Is that please correct?

Yes, but it would be better if you rephrased your statement to more clearly match the definition of an eigenvector and eigenvalue:
Suppose $\lambda$ and $\vec v$ are eigenvalue and eigenvector of $A$, respectively. For any $t \in \mathbb{R}$, where $t \ne 0$, $A( \vec {tv}) = t A\vec v = t \lambda \vec v = \lambda \vec {tv}$. So $\vec {tv}$ is also an eigenvector of $A$ with the eigenvalue $\lambda$.

 

[member 731016]

Yes, but it would be better if you rephrased your statement to more clearly match the definition of an eigenvector and eigenvalue:
Suppose $\lambda$ and $\vec v$ are eigenvalue and eigenvector of $A$, respectively. For any $t \in \mathbb{R}$, where $t \ne 0$, $A( \vec {tv}) = t A\vec v = t \lambda \vec v = \lambda \vec {tv}$. So $\vec {tv}$ is also an eigenvector of $A$ with the eigenvalue $\lambda$.

Thank you for your help @FactChecker!

 

[FactChecker]

Thank you for your help @FactChecker!

Actually, I realize that your statement did match the definitions of eigenvector and eigenvalue, but I think that I have rephrased it more as a step-by-step proof.

 

[member 731016]

Actually, I realize that your statement did match the definitions of eigenvector and eigenvalue, but I think that I have rephrased it more as a step-by-step proof.

Thank you for your reply @FactChecker! Yeah I only just realized the definition of eigenvector is for a value of $\lambda$ not the matrix A too!

 

[FactChecker]

Thank you for your reply @FactChecker! Yeah I only just realized the definition of eigenvector is for a value of $\lambda$ not the matrix A too!

It's for the combination of the matrix, $A$, and the eigenvalue $\lambda$

 

[member 731016]

It's for the combination of the matrix, $A$, and the eigenvalue $\lambda$

Oh, thank you for you letting me know @FactChecker !