- #1
Mayhem
- 351
- 249
Is it possible (read: reasonably easy) to find global minima of an nth degree polynomial of the general form $$a_nx^n + a_{n-1}x^{n-1} ... a_2x^2 +a_1x + a_0 = 0$$ It seems to have applications in computational chemistry as I have a "hunch" that polynomial regression could be used to somewhat accurately predict the lowest conformational energy levels of complicated molecules.
Inspiration for this hunch:
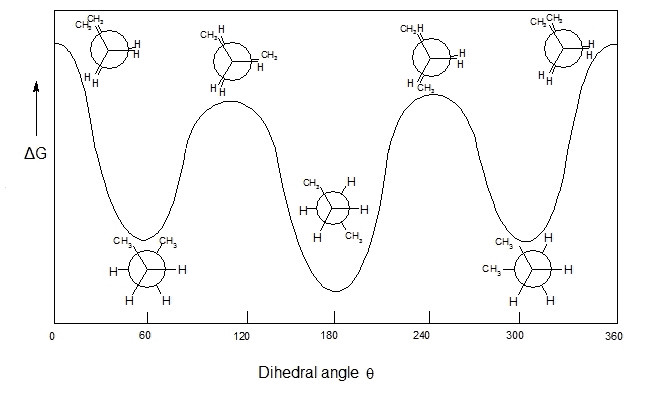
Finding extrema for a given polynomial requires finding zeroes of its first derivatives. I heard this gets difficult quickly.
Any input? This is purely out of curiosity.
Inspiration for this hunch:
Finding extrema for a given polynomial requires finding zeroes of its first derivatives. I heard this gets difficult quickly.
Any input? This is purely out of curiosity.
Last edited: