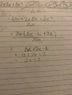- #1
Finding Limits with DeltaX: An Essential Tool for Calculus
- Thread starter Witcher
- Start date
-
- Tags
- Limit
In summary, DeltaX is a small increment or change in the input value of a function that is used in the process of finding a limit. The specific value of DeltaX is typically chosen to be a small number, but it can be negative and depends on the function and point being evaluated. While DeltaX is a common method for finding limits, there are other approaches and limitations to consider, such as its potential for inaccurate approximations and its applicability to certain types of functions.
FAQ: Finding Limits with DeltaX: An Essential Tool for Calculus
1. How does DeltaX help in finding a limit?
DeltaX, also known as the change in x, is used in the limit definition to find the slope of a curve at a specific point. By taking smaller and smaller values for DeltaX, we can approach the exact value of the limit.
2. What is the significance of finding a limit using DeltaX?
Finding a limit using DeltaX helps us understand the behavior of a function at a specific point. It also helps us determine the slope of a curve and the rate of change of a function.
3. Can DeltaX be any value when finding a limit?
No, DeltaX must approach 0 in order for the limit to be accurate. This means that we must take smaller and smaller values for DeltaX, but it can never be equal to 0.
4. Are there any limitations to using DeltaX to find a limit?
Yes, DeltaX is not always the most efficient method for finding limits. In some cases, we may need to use other techniques such as L'Hopital's rule or the squeeze theorem.
5. How do we know if we have found the correct limit using DeltaX?
We can check our answer by plugging in the limit value into the function and seeing if it matches the value obtained through the DeltaX method. We can also use graphing tools to visualize the behavior of the function and confirm our result.