member 731016
- Homework Statement
- Please see below
- Relevant Equations
- Please see below
For this problem,

The solution is,
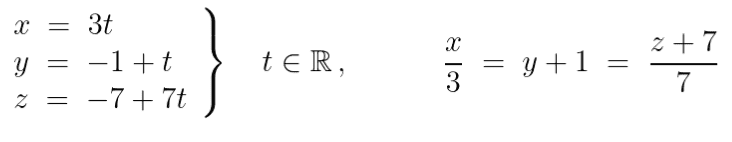
However, I could not get that. By getting the system in REF, I got ##x = 3 + \frac{3}{7}z ## and ##y = \frac{1}{7}z##. Therefore z is a free variable so ##x = 3 + \frac{3}{7}t = 0## and ##y = \frac{1}{7}t##.
Thus equation of line is ##x\hat i + y\hat j + z\hat k = 3\hat i + (\frac{3}{7}\hat i + \frac{1}{7}\hat j)t##
Does anybody please know what I did wrong here?
Many thanks!
The solution is,
However, I could not get that. By getting the system in REF, I got ##x = 3 + \frac{3}{7}z ## and ##y = \frac{1}{7}z##. Therefore z is a free variable so ##x = 3 + \frac{3}{7}t = 0## and ##y = \frac{1}{7}t##.
Thus equation of line is ##x\hat i + y\hat j + z\hat k = 3\hat i + (\frac{3}{7}\hat i + \frac{1}{7}\hat j)t##
Does anybody please know what I did wrong here?
Many thanks!
Last edited by a moderator: