- #1
VishalChauhan
- 30
- 1
Homework Statement
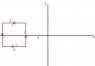
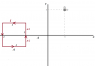
A square wire frame,in the x-y plane, carrying a current 'I' and with side length 'A' is kept at a distance 'A' from the y-axis . Find the magnetic flux through the other half of the plane(not containing the square loop).
Homework Equations
The magnetic field due to line charge is μi/4πr(sinø1+sinø2)
The magnetic field due to a dipole is μM/2πl3
The Attempt at a Solution
I tried to find the magnetic field at a given distance from from the loop,but it was too clumsy.Symmetry considerations won't work(though i guess its the only way to solve this problem)