- #1
maxalador
- 25
- 0
Homework Statement
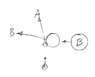
Ball A with mass 4 kg is moving with a velocity of 8 m/s North when it crashes into Ball B with unknown mass moving with a velocity of 6 m/s West. This collision is perfectly elastic. If Ball A ends up moving with a velocity of 6.5 m/s @ 120° after the collision, find the mass and final speed of Ball B if it moves at an angle of 160° after the collision.
Homework Equations
m1v1 + m2v2 = m1v1’ + m2v2’
The Attempt at a Solution
I'm not sure how to start the problem but I think you take the starting velocities and angles and use sine and cosine to find their x and y components