Finding max elastic energy of a bow

[spanky489]

Hi guys, I am trying to find the theoretical maximum elastic energy of a bow with a constant square cross section with its moment of inertia I, made from a homogenous material throughout the whole length so we can say that the Youngs modulus E is also constant. This bow is attached to a string on both ends and to simplify the problem let's say that the forces pulling both ends are always transverse/tangential in reference to the cross section.

This is the first thing I am trying to calculate and is also the prerequisite to calculating the maximum initial velocity of the arrow being launched by the bow.

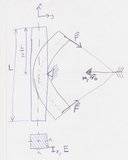
i know that i need to find the yield strength of the material and through Hooke's law solve the force that causes the maximum strain. The problem I am facing is that i do not know which theory to apply to this problem. If the deflections weren't so big i would use the euler-bernoulli equations but since that won't work here i was thinking of using the von karman strains.

while searching for information i came across this doctors dissertation which could also be useful in my case but I am not sure how it fares with von karman strains in this situation.

any help at all will be appreciated.

thanks
spanky

 

[Achy47]

Hi spanky,

To find the maximum elastic energy of the bow, you can use the formula for elastic potential energy: PE = 1/2 * k * x^2, where k is the spring constant and x is the displacement from the equilibrium position. In this case, the spring constant can be calculated using Hooke's law: F = k * x, where F is the force applied to the bow and x is the displacement.

To find the maximum strain, you can use the formula for strain: ε = ΔL/L, where ΔL is the change in length and L is the original length. The force that causes the maximum strain is the yield strength of the material.

As for which theory to apply, it would depend on the specific properties of the material and the geometry of the bow. Both the Euler-Bernoulli equations and the von Karman strains can be used, but it would be best to consult with a materials expert or perform some experiments to determine the most accurate approach for your specific case.

I hope this helps. Good luck with your calculations!