gevni
- 25
- 0
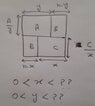
I have a formula for cost calculation that contain x and y two variable. I have to find the value of (x,y) where that formula will gives minimum value as cost should not be equal to zero, it has some minimum value.
I took 1st partial derivative with respect to x and then with y and found the value of x and y where function will give minimum value. My question is how to combine both to get one answer as optimal (x,y) where function has minimum cost?
I took 1st partial derivative with respect to x and then with y and found the value of x and y where function will give minimum value. My question is how to combine both to get one answer as optimal (x,y) where function has minimum cost?
Last edited: