Finding Missing Angle Within A Triangle

In summary, the conversation is about a user seeking help with a geometry challenge problem. They are asked to show their progress so far and the conversation discusses finding a solution using only geometry. The user is reminded of the forum rules and asked to refrain from bumping their thread in the future.
  • #1
ychst
4
0
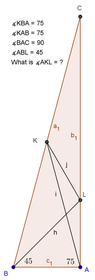
View attachment 6539

Can someone please help me with this question? Any help would be really much appreciated. Thanks all and have a great Easter!
 

Attachments

  • untitled.png
    untitled.png
    9.3 KB · Views: 82
Mathematics news on Phys.org
  • #2
Re: Geometry challenge problem

Hello ychst and welcome to MHB! :D

We ask that our users show their progress (work thus far or thoughts on how to begin) when posting questions. This way our helpers can see where you are stuck or may be going astray and will be able to post the best help possible without potentially making a suggestion which you have already tried, which would waste your time and that of the helper.

Can you post what you have done so far?

Also, please do not post duplicates of the same problem. :)
 
  • #3
Re: Geometry challenge problem

Hi Greg, thank you for your reply. Apologies for posting in different forums. I initially thought it would be seen be people with different interest/expertise. Below is my attempt at solving the problem. I am trying to validate whether my answer is correct. Thank you. View attachment 6542
 

Attachments

  • answer.png
    answer.png
    22.3 KB · Views: 83
  • #4
Re: Geometry challenge problem

That's correct. Good work. I suppose the challenge now is to find a solution that only uses geometry. :)
 
  • #5
Re: Geometry challenge problem

Exactly, that's what I'm kind of stuck on. Does anyone have a pure geometry solution?
 
  • #6
Re: Geometry challenge problem

Does anyone have a pure geometry answer to this question?
 
  • #7
Re: Geometry challenge problem

Hello ychst,

MHB rule #1 states:

MHB Rules said:
No bumping. Bumping a thread is posting a reply to that thread solely to raise its profile and return it to the top of the active threads list. This is forbidden at MHB. If you want to draw attention to an unanswered thread, then post something of value such as further progress. It is also forbidden to bump one thread by drawing attention to it in a different thread.

This rule is designed to make MHB more useful and efficient for everyone. When you bump a thread this adds no content and yet draws attention to it, causing people to possibly take time to see what has been added only to find that no content has actually been added. This can waste the time of our helpers, and this time is very valuable. Any time we can save on the part of the volunteer helpers would, I hope you can see, help you in the long run! So, if you could please help us help you in this way, by not bumping, we would greatly appreciate it.

We ask that you be patient and wait for someone to reply. You are of course welcome to post your progress or additional thoughts that have occurred in the meantime.

We ask that you keep this policy in mind in the future. We also ask that you consider how much less efficient MHB would be if this posting behavior was allowed.

greg1313
 

FAQ: Finding Missing Angle Within A Triangle

How do you find a missing angle within a triangle?

To find a missing angle within a triangle, you can use the fact that the sum of all angles in a triangle is 180 degrees. This means that if you know the measure of two angles, you can subtract their sum from 180 to find the missing angle.

Can you use the Pythagorean Theorem to find a missing angle in a triangle?

No, the Pythagorean Theorem is used to find the length of a side in a right triangle, not the measure of an angle. To find a missing angle in a triangle, you need to use the properties of triangles and their angles.

What is the sum of the angles in a triangle?

The sum of the angles in a triangle is always 180 degrees. This is a fundamental property of triangles and is true for all types of triangles, whether they are equilateral, isosceles, or scalene.

Can you use trigonometry to find a missing angle in a triangle?

Yes, you can use trigonometry to find a missing angle in a triangle if you know the lengths of two sides. By using the sine, cosine, or tangent functions, you can find the measure of the missing angle using the side lengths and the Pythagorean Theorem.

Are there any special cases where finding a missing angle in a triangle is easier?

Yes, if you have a right triangle, you can use the trigonometric ratios (sine, cosine, tangent) to find the missing angle more easily. Additionally, if you have an equilateral triangle, all three angles will be equal, making it very easy to find the measure of any missing angle.

Similar threads

MHB Can You Find the Angle in This Isosceles Triangle Problem?
Replies
1
Views
1K
B A Question Relating Sum of Angles and Breaking of the Parallel Postulate
Replies
6
Views
1K
I Help with area formula using direction cosines
Replies
3
Views
268
MHB Find $\angle B$ for Triangle $ABC$ with Bisectors $AD,BE$
Replies
1
Views
959
MHB What are the angles of isosceles triangle ABC?
Replies
1
Views
959
MHB Acute angle of right triangles
Replies
4
Views
1K
MHB Can an Ellipse Help Solve the Scalene Triangle Problem?
Replies
1
Views
957
MHB Find Length of Side in Right Triangle w/ 45°, 90°, and 45° Angle
Replies
2
Views
1K
I Finding vertex of a 3D Triangle on a Plane
Replies
3
Views
1K
MHB Problem about equilateral triangles
Replies
2
Views
1K

Hot Threads

Recent Insights

Back
Top