pairofstrings
- 411
- 7
- TL;DR Summary
- Online app for arranging terms with P.E.M.D.A.S.
Hello. I have an equation that looks like following:
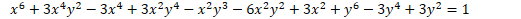
I want to re-write the terms of the above equation adhering to PEMDAS.
I have seen the web but I could find none.
Thanks.
I want to re-write the terms of the above equation adhering to PEMDAS.
I have seen the web but I could find none.
Thanks.