- #1
Chrono G. Xay
- 92
- 3
I really don't have much experience with calculus ( :sarcasm: Hooray! ), but earlier I was reading an introductory article explaining the usefulness of the Lagrange multiplier in dimensional optimization,
http://www.slimy.com/~steuard/teaching/tutorials/Lagrange.html
and it reminded me that another curiosity of mine is trying to find the optimal point along which one could pivot a drumstick, whose shape I will define as:
a relatively thin cylinder, with a half-sphere on the 'butt end', and on the other a paraboloid, whose tip is partially overlapped by a smaller shape- be it an ellipsoid, a barrel-esque shape (haha, burlesque), or a sphere. For the sake of argument it is made of an isotropic material.
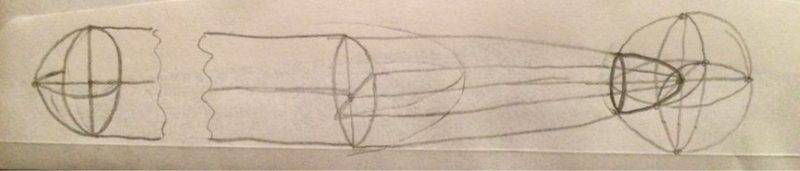
(This picture obviously does not use the correct proportions of scale, but I hope it gets the general point across)
I really don't have much experience with adding and subtracting volumes for computing that of a... object of 'composite shape'(?) (my words), but while the cylinder and half-sphere are quite straightforward, I'm pretty sure that in order to find the total volume for such an object I'm going to need to 1) subtract a spherical/ellipsoidal cap from the paraboloid, and 2) subtract the tip of the paraboloid from the sphere/ellipsoid.
I went ahead and wrote the volumes of each shape below:
Vcylinder = πrc2hc
Vsphere = \frac{4}{3}πrs3
Vparaboloid = \frac{π}{2}hprp2
Vellipsoid = \frac{4}{3}πrMrm2
Vs,cap = \frac{πh2}{3}(3rs-h)
Ve,cap = πrm2(\frac{2}{3}rM - h + \frac{h3}{3rM2})
(It occurred to me to do it this way by intuition, visualizing how the boundaries of the paraboloid and sphere/ellipsoid intersect each other. I also realize that the volume of a shape could also be calculated in two dimensions, of which the Cartesian integral is taken from 0 to Lnet , followed by the polar integral from 0 to 2π.)
Note: The phrases "Cartesian integral" and "polar integral" are my own, simply because I either do not know or do not recall the 'official' terminology for these methods.
Anyway, I know that there need to be some particular constraints: to minimize the moment of inertia, yet maximize the potential angular momentum when moving through an arc of
s = \frac{πra}{2}
where
ra = \frac{Lstick - CoM}{2}+d
CoM is the center of mass along the stick's length, and d is the distance between the axis of rotation and the stick's center of mass along its length, and the axis of rotation must also lie along the stick's length. (I apologize for the repetition of phrase- I'm not sure how else to word it at the moment)
Now the parallel axis theorem states:
I = ICoM + Md2 ,
so the 'optimal' moment of inertia will lie somewhere between \frac{1}{12}ML2 and \frac{1}{3}ML2, with a corresponding distance d .
Could one not use the idea of the Lagrange multiplier to find the answer for a question such as this?
In the past I had considered the trebuchet as being a good study for optimizing the location of the pivot, but even then the best I could find online was an approximation which assumed a beam with unchanging dimensions throughout its length.
http://www.slimy.com/~steuard/teaching/tutorials/Lagrange.html
and it reminded me that another curiosity of mine is trying to find the optimal point along which one could pivot a drumstick, whose shape I will define as:
a relatively thin cylinder, with a half-sphere on the 'butt end', and on the other a paraboloid, whose tip is partially overlapped by a smaller shape- be it an ellipsoid, a barrel-esque shape (haha, burlesque), or a sphere. For the sake of argument it is made of an isotropic material.
(This picture obviously does not use the correct proportions of scale, but I hope it gets the general point across)
I really don't have much experience with adding and subtracting volumes for computing that of a... object of 'composite shape'(?) (my words), but while the cylinder and half-sphere are quite straightforward, I'm pretty sure that in order to find the total volume for such an object I'm going to need to 1) subtract a spherical/ellipsoidal cap from the paraboloid, and 2) subtract the tip of the paraboloid from the sphere/ellipsoid.
I went ahead and wrote the volumes of each shape below:
Vcylinder = πrc2hc
Vsphere = \frac{4}{3}πrs3
Vparaboloid = \frac{π}{2}hprp2
Vellipsoid = \frac{4}{3}πrMrm2
Vs,cap = \frac{πh2}{3}(3rs-h)
Ve,cap = πrm2(\frac{2}{3}rM - h + \frac{h3}{3rM2})
(It occurred to me to do it this way by intuition, visualizing how the boundaries of the paraboloid and sphere/ellipsoid intersect each other. I also realize that the volume of a shape could also be calculated in two dimensions, of which the Cartesian integral is taken from 0 to Lnet , followed by the polar integral from 0 to 2π.)
Note: The phrases "Cartesian integral" and "polar integral" are my own, simply because I either do not know or do not recall the 'official' terminology for these methods.
Anyway, I know that there need to be some particular constraints: to minimize the moment of inertia, yet maximize the potential angular momentum when moving through an arc of
s = \frac{πra}{2}
where
ra = \frac{Lstick - CoM}{2}+d
CoM is the center of mass along the stick's length, and d is the distance between the axis of rotation and the stick's center of mass along its length, and the axis of rotation must also lie along the stick's length. (I apologize for the repetition of phrase- I'm not sure how else to word it at the moment)
Now the parallel axis theorem states:
I = ICoM + Md2 ,
so the 'optimal' moment of inertia will lie somewhere between \frac{1}{12}ML2 and \frac{1}{3}ML2, with a corresponding distance d .
Could one not use the idea of the Lagrange multiplier to find the answer for a question such as this?
In the past I had considered the trebuchet as being a good study for optimizing the location of the pivot, but even then the best I could find online was an approximation which assumed a beam with unchanging dimensions throughout its length.
Last edited: