- #1
Saladsamurai
- 3,020
- 7
!Shear Diagram!
I have posted the problem below. I am looking to find P max. My professor wants us to draw a shear diagram to find out where it will occur.
From equilibrium equations I have found that Ay=By=P+0.6 kip
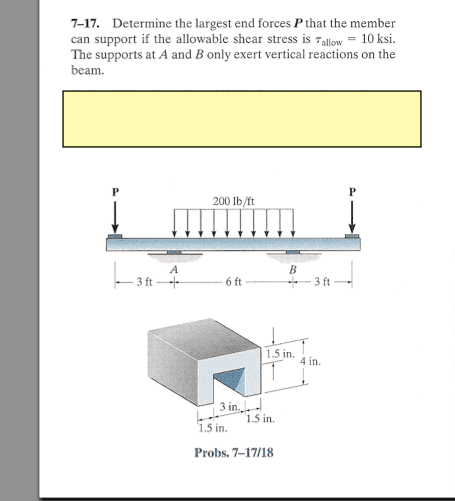
I am having trouble drawing the diagram. I know it starts with -P and is constant until it hits Ay. Then I add -P+(P+.6) So it is +.6
Now there is a distributed load. So it should decrease linearly. But that is where I am stuck. Where does it decrease to? Does it cross the x-axis at all? Sorry, but I just can't see this one straight...
Homework Statement
I have posted the problem below. I am looking to find P max. My professor wants us to draw a shear diagram to find out where it will occur.
From equilibrium equations I have found that Ay=By=P+0.6 kip
I am having trouble drawing the diagram. I know it starts with -P and is constant until it hits Ay. Then I add -P+(P+.6) So it is +.6
Now there is a distributed load. So it should decrease linearly. But that is where I am stuck. Where does it decrease to? Does it cross the x-axis at all? Sorry, but I just can't see this one straight...