- #1
mariya259
- 17
- 0
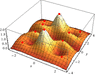
I have the function:
f(x,y)= x*(y^2)*e^-((x^2+y^2)/4)
I am not sure how to find the point where the gradient is the greatest.
The gradient I found after taking the partials is:
partial with respect to x: e^(-(x^2+y^2)/4)*((y^2)-.5(x^2)(y^2))
partial with respect to y:e^(-(x^2+y^2)/4)*(2yx-.5x(y^3))
What do I do next?
(I have also found min/max points for this function)
f(x,y)= x*(y^2)*e^-((x^2+y^2)/4)
I am not sure how to find the point where the gradient is the greatest.
The gradient I found after taking the partials is:
partial with respect to x: e^(-(x^2+y^2)/4)*((y^2)-.5(x^2)(y^2))
partial with respect to y:e^(-(x^2+y^2)/4)*(2yx-.5x(y^3))
What do I do next?
(I have also found min/max points for this function)