Finding Polar Region Between r=2 and r=4cos(theta)

[Pindrought]

I'm really stumped here as usual. Here is what I've managed to figure out.

I'm given two equations.
r=2
r=4cos(theta)I converted them both to rectangular coordinates to get an idea of what the graph would look like.

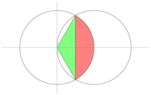
I need to find either the area in red or the area in green. (In this case, I tried to find the area in green) .If I have the area in red or green, I know that I can just subtract one of them from pi*r^2 which in this case would be 4pi to get the area of the other section.

The problem I am facing right now is setting up the integral the proper way. I was thinking of going about it like this.

So a few questions. First, did I approach this in a correct way? Second, how would I know how to set this up to solve the integral using polar coordinates instead of converting it all to rectangular form?

Thanks for taking the time to answer, I tried to make this as clear as possible to see where I'm making my mistake or what I should be doing differently.

 

[Opalg]

I would prefer to do this problem using geometry rather than calculus.

View attachment 2178​

The red area here is one half of the area that you are looking for. The two circles intersect at the points $(1, \pm\sqrt3)$ (by Pythagoras). So the red and green regions together form a $120^\circ$ sector equal to one-third of the left circle. Thus the red and green regions have a combined area $\dfrac{4\pi}3.$ The green triangle has area (half base times height) $\sqrt3.$ So the red region has area $\dfrac{4\pi}3 - \sqrt3.$ The area that you want is twice the area of the red region, namely $\dfrac{8\pi}3 - 2\sqrt3.$

So your answer is correct (and of course the calculus method is just as valid as the geometric method).

 

[johng1]

Hi,
You wanted to know how to do this using polar coordinates and polar areas. The attachment shows how to do this:

View attachment 7769