Finding roots of this particular polynomial

[JackDaniel87]

Hey guys,

Nice to be on here.
I have been banging my brain for the last two weeks trying to come up with an algebraic solution to the following question - to no avail.
Any input would be MUCH appreciated!
The problem is somewhat long but can be summarized as follows:

Begin with the following equation as a function of x. There are two parameters, a and b, that could take on arithmetic values but I am more interested in a general solution:

[math]y(x)=\frac{b\left(1-x\right)}{b\left(1-x\right)+\left(1-a\right)x}[/math]

The curvature K of the above polynomial ought to be given by the the following differential equation which uses the first and second order derivatives of y(x), as follows:

\[ k= \frac{|\frac{d^2y}{dx^2}|}{[1 + (\frac{dy}{dx})^2]^\frac{3}{2}} \]

Now, I am actually interested in the maximum curvature k - which is why we need to differentiate k with respect to x and find its roots:

[math]𝑘′=\frac {d}{dx}k[/math]

Hence, I am interested in finding the roots of k' as a function of a and b, particularly for values of x between 0 and 1. I know a solution exists because graphically it is evident, as seen here, where the purple line (k') crosses the x-axis:

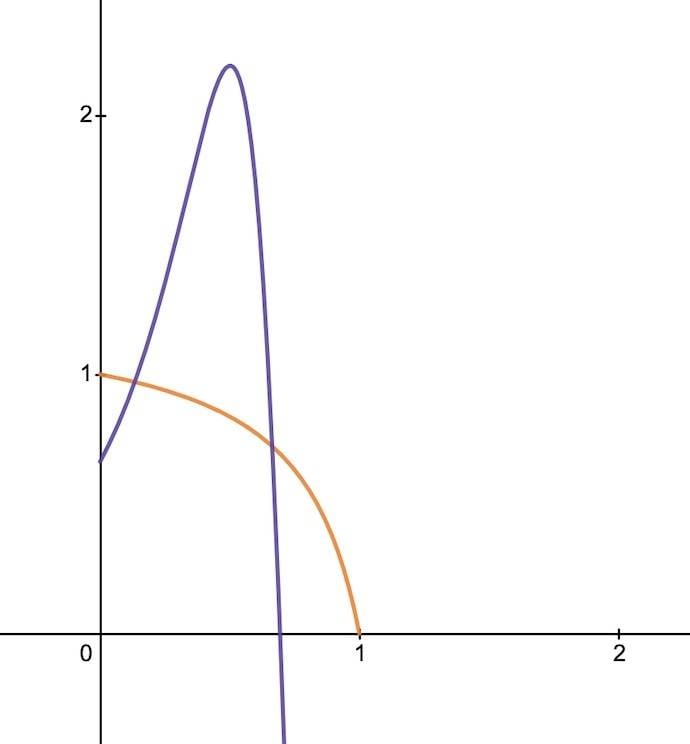
However, obtaining an algebraic solution as a function of a and b has been a challenge - hence my reaching out!

Any input you might have would be GREATLY appreciated!

Thank you in advance for any help you may offer!

-J

 

[HOI]

First, that is NOT a polynomial. In any case have you found [math]\frac{dy}{dx}[/math] and [math]\frac{d^2y}{dx^2}[/math]? That should be your first step.

 

[JackDaniel87]

Fine… if you’re in the field where division of polynomials isn’t a polynomial expression…regardless, when you derive the expression, the ensuing curvature equation doesn’t lend itself (in my limited experience) to finding the roots easily. Any leads?

 

[HOI]

Fine… if you’re in the field where division of polynomials isn’t a polynomial expression…

In what field is that NOT true? The result of the "division of polynomials" is a "rational function".

Please show the equation you got for the curvature function.

 

[JackDaniel87]

Biostatistics you can multiply two polynomials one of which is to the power of -1. In any case, terminology aside: here's the equation for curvature:

\[ k= \frac{\left|-\frac{2b\left(a-1\right)\left(-b+1-a\right)}{\left(b\left(1-x\right)+x\left(1-a\right)\right)^{3}}\right|}{\left[1+\left(\frac{b\left(a-1\right)}{\left(b\left(1-x\right)+x\left(1-a\right)\right)^{2}}\right)^{2}\right]^{\frac{3}{2}}} \]