Finding support for multivariate transformation

[lemonthree]

For the given joint pdf of X and Y $$f(x,y) = 12xy(1 - y); 0 < x < 1;
0 < y < 1$$
Let $Z = XY^2$ and $W = Y$ be a joint transformation of (X,Y)

Sketch the graph of the support of $(Z,W)$ and describe it
mathematically.

I'm not very sure how to describe (Z,W).
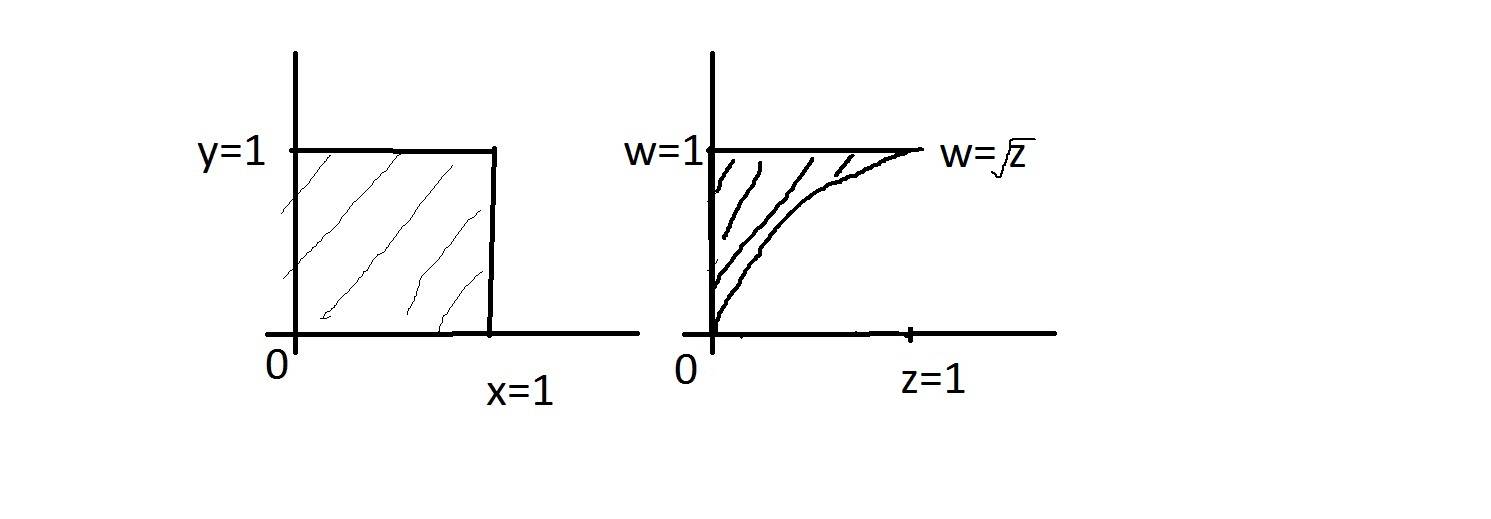
First, I draw the graph of the support of X and Y, which is a rectangular support.

Now I "map" each interval over to (Z,W).

For $x=0, 0<y<1, z=0, 0<w<1$

For $x=1, 0<y<1, 0<z<w^2, 0<w<1 $

For $y=0, 0<x<1, z=0, w=0$

For $y=1, 0<x<1, 0<z<1, w=1 $

I'm not quite sure how to describe (Z,W), this isn't rectangular neither is it triangular. I have drawn the graph of what I think is the support of (Z,W). How do I describe this quadrant-like support? $0<w<1, 0<z<1, \sqrt{z}<w<1$?

 

[lemonthree]

After some figuring out, I determined that the description of the support is all as described in the graph drawn. $0 < \sqrt{z} < w < 1$