happyparticle
- 490
- 24
- Homework Statement
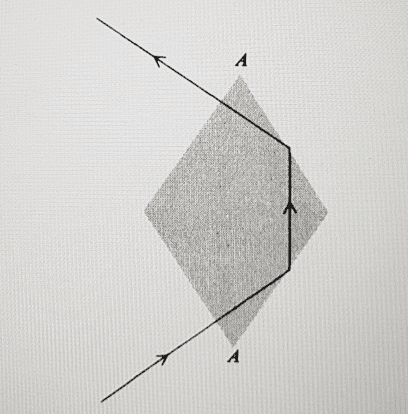
- Finding the angle at the apex (A) for which the outgoing beam is perpendicular to the side of a rhomb if the incoming plane wave is linearly polarized at 45 degrees to the plane of incidence and the beam is perpendicular to the first side.
- Relevant Equations
- ##\theta_I = \theta_t = 0##
Hi,
Since I'm dealing with a rhombus, the angle at the bottom(A) and top(A) are the same. Thus, I only have to find the angle at the bottom since the incoming beam is already perpendicular to the side of the rhombus.
Since the incoming beam is perpendicular to the side ##\theta_I = \theta_T = 0## If I understood correctly.
And it seems to have no reflection.
I'm not sure if all those details are important to find the angle. However I can't put those pieces together.
It might be simple, but for some reasons I don't know how to begin.
Any help will be appreciate
Thanks
Since I'm dealing with a rhombus, the angle at the bottom(A) and top(A) are the same. Thus, I only have to find the angle at the bottom since the incoming beam is already perpendicular to the side of the rhombus.
Since the incoming beam is perpendicular to the side ##\theta_I = \theta_T = 0## If I understood correctly.
And it seems to have no reflection.
I'm not sure if all those details are important to find the angle. However I can't put those pieces together.
It might be simple, but for some reasons I don't know how to begin.
Any help will be appreciate
Thanks