Finding the area of a region which is inside two circles (II)

[shamieh]

Decided to make a new thread so it wouldn't be jumbled up with the other thread I posted about this particular problem.

Question: Find the area of the region which is inside both $$r = 2$$ and $$ r = 4sin(\theta)$$

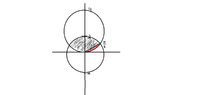
So solving, I know that $$sin\theta = \frac{1}{2}$$. I also sketched a picture and found that the sides were symmetrical.

View attachment 2169

Here is how I am seeing the problem. I know that $$sin\theta = 1/2$$ at $$\frac{\pi}{6}$$

Noticing that we can cut out a slice where the curve intersects

So I set up my first integral as:

$$2 [ \int^{\frac{\pi}{6}}_0 \frac{1}{2} [4\sin\theta]^2 ] \, d\theta$$

After integrating this I obtain: $$\frac{2\pi}{3} - 2\sqrt{3}$$

I was then told that the remaining area in the circle on the side that we are calculating is $$\frac{4\pi}{6}$$ because $$\frac{1}{6}$$ of $$180$$ is $$\frac{\pi}{6}$$.. I understand that 1/6 of 180 is 30 degrees or $$\frac{\pi}{6}$$ .. What I don't understand is where does the 4 come from?

Also, here is what I obtained for my final result noting that I multiplied the whole thing by 2 since it was symmetrical.

My result: $$A = \frac{8\pi}{3} - 4\sqrt{3}$$

 

[Pindrought]

I'm also trying to figure this problem out. I tried converting both equations to rectangular form, and finding where they intersect.

I got the points of intersection were sqrt(3) and -sqrt(3)

I set up my integral as $$\int^{\sqrt{3}}_{-\sqrt{3}} 2*\sqrt{4-x^2} -2 \, dx$$

Am I wrong in assuming I can do this and get the correct result? My final answer was 8arcsin(3) which is approximately 12.566

 

[MarkFL]

I think I would approach it a bit differently, and use:

$$A=4\pi-\int_{\frac{\pi}{6}}^{\frac{\pi}{2}}16 \sin^2(\theta)-4\,d\theta=4\pi-\frac{4}{3}\pi-2\sqrt{3}=\frac{8}{3}\pi-2\sqrt{3}$$

I am taking the area of one of the circles, and then subtracting from this the area inside the upper circle but outside the lower circle. ;)

If we want to approach it using rectangular coordinates and symmetry, then we have:

$$A=4\int_0^1\sqrt{4-(y-2)^2}\,dy$$

And we get the same result.

 

[shamieh]

I think I would approach it a bit differently, and use:

$$A=4\pi-\int_{\frac{\pi}{6}}^{\frac{\pi}{2}}16 \sin^2(\theta)-4\,d\theta=4\pi-\frac{4}{3}\pi-2\sqrt{3}=\frac{8}{3}\pi-2\sqrt{3}$$

I am taking the area of one of the circles, and then subtracting from this the area inside the upper circle but outside the lower circle. ;)

.

So are you saying this? View attachment 2170

 

[Pindrought]

I think I would approach it a bit differently, and use:

$$A=4\pi-\int_{\frac{\pi}{6}}^{\frac{\pi}{2}}16 \sin^2(\theta)-4\,d\theta=4\pi-\frac{4}{3}\pi-2\sqrt{3}=\frac{8}{3}\pi-2\sqrt{3}$$

I am taking the area of one of the circles, and then subtracting from this the area inside the upper circle but outside the lower circle. ;)

If we want to approach it using rectangular coordinates and symmetry, then we have:

$$A=4\int_0^1\sqrt{4-(y-2)^2}\,dy$$

And we get the same result.

I can't figure out what I did wrong, because I got ~12.566 for my integral and I got ~4.9 for the rectangular coordinate integral you posted.(Wondering) Do you have any good links to example problems for this type of problem?

 

[MarkFL]

If we take the area of the upper circle, and subtract away from this the area inside the upper circle but not in the lower circle, then we get the area simultaneously inside both, i.e., the intersection of the two circles. Hence we have:

$$A=\pi(2)^2-\left(2 \left(\frac{1}{2}\int_{\frac{\pi}{6}}^{\frac{\pi}{2}} \left(4\sin(\theta) \right)^2\,d\theta- \frac{1}{2}\int_{\frac{\pi}{6}}^{\frac{\pi}{2}} \left(2 \right)^2\,d\theta \right) \right)$$

Now, this can be rewritten as:

$$A=4\pi-4\int_{\frac{\pi}{6}}^{\frac{\pi}{2}} 4\sin^2(\theta)-1\,d\theta$$

Using a double-angle identity for cosine, then we may write:

$$A=4\pi-4\int_{\frac{\pi}{6}}^{\frac{\pi}{2}} 1-2\cos(2\theta)\,d\theta$$

Applying the FTOC, we obtain:

$$A=4\pi-4\left[\theta-\sin(2\theta) \right]_{\frac{\pi}{6}}^{\frac{\pi}{2}}=4\pi-4\left(\frac{\pi}{2}-\frac{\pi}{6}+\frac{\sqrt{3}}{2} \right)=\frac{8}{3}\pi-2\sqrt{3}$$

 

[shamieh]

Wow Brilliant. I was forgetting to double it. My god the algebra involved lol. Thanks for the help!