- #1
Illusionist
- 34
- 0
Homework Statement
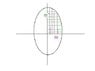
Find the area of the region bounded by the positive x-axis,
the positive y-axis and the curve:
(x^2) +[(y^2)/4] = 1
using vertical and horizontal strips.
Homework Equations
Basically I just tried to use integration to find the area, but I suspect I have made a mistake about what the interval for the integration should be.
The Attempt at a Solution
Vertical Strips -
Transposing the equation gives me: y=Sqrt[1-(x^2)]
So basically I know that the area would be the integral of this but not 100% sure between what intervals. I suspect, from a graph obtained from a graphics calculator, that is between 1 and -1.
Hence area= Integral of Sqrt[1-(x^2)] between 1 and -1.
The integral I got to be Sqrt[1-(x^2)]x + arcsin(x), from a online integration calculator. Between 1 and -1 this would give a area of Pi.
Horizontal Strips -
Transposing the equation gives me: x=Sqrt[1-[(y^2)/4])
Now the integral of this I got to be [(1/4)Sqrt(4-(y^2))].y + arcsin(y/2)
From the same graph I assume the interval for this one should be from 2 to 0. But substituting these values gives me a area of (Pi/2).
Obviously the areas need to be the same and they aren't! I'm positive that it is the intervals for integration that I am having trouble with, but where the mistake is and why I am not sure. My only guess is that becaise it says positive x and y-axis that the interval for the vertical strips should be 1 to 0, but not sure and would this approach change anything I did for the horizontal? Any help or advice would be great. Thanks guys!