Finding the Axis of Rotation with Given CoG and Force Point

[pointdexter16]

TL;DR Summary

I want to determine the axis of rotation of a body which is falling under the influence of gravity and an external force is acting on a specific point on it.

[Mentor Note: See post #10 below for an updated problem statement using LaTeX and with a better drawing]

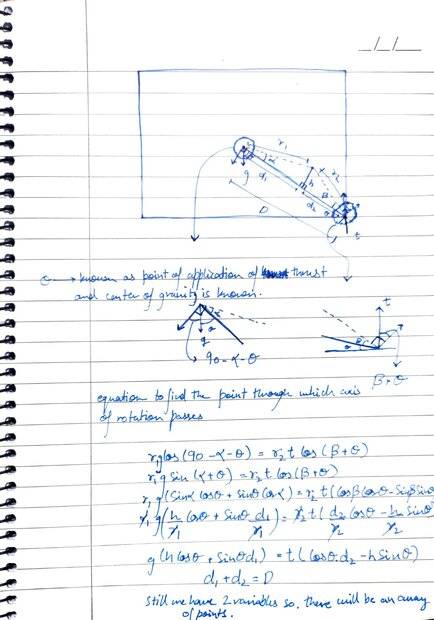
what i want is to find the axis of rotation when the centre of gravity and point on which external force is acting is given along with the magnitude and direction of force. In the example that i used to illustrate the above problem i have taken a simple case where centre of gravity is the centre of the square as mass is uniformly distributed and the point where external force is acting is the bottom left corner of the square.When i was looking for how to determine the axis of rotation it was given that it passes through the point where the torque produce by both gravity and external force is zero therefore making it a point which won't go through rotational motion.Now i tried to determine the point my solving the equation but i ended but with 2 variable in the end which concludes that there will an array of points which intern means that there will be multiple axis of rotation though i believe that i am making some mistake cause intuitively i feels like there should only be one.i am open to other approaches to this problem.please excuse me for my sloppy writing .Thank you

 

[berkeman]

Welcome to PF.

Please excuse me for my sloppy writing .Thank you

For future posts, please see the "LaTeX Guide" link below the Edit window. That will help you post math equations here at PF. Thanks.

 

[Vanadium 50]

I can't follow the sketch (so I agree with @berkeman ) but let me ask you two questions:
1. What is the torque on the object?
2. What is its center of mass?

 

[Lnewqban]

Welcome, @pointdexter16 !

Why is the center of mass located all the way to the left end of the falling body?
It is very hard to see your diagram, sorry.

I am referring to "centre of gravity is the centre of the square as mass is uniformly distributed and the point where external force is acting is the bottom left corner of the square."

May it be bottom right corner instead?

 

[pointdexter16]

Welcome to PF. For future posts, please see the "LaTeX Guide" link below the Edit window. That will help you post math equations here at PF. Thanks.

ohh thank you will keep in mind

 

[pointdexter16]

Welcome, @pointdexter16 !

Why is the center of mass located all the way to the left end of the falling body?
It is very hard to see your diagram, sorry.

I am referring to "centre of gravity is the centre of the square as mass is uniformly distributed and the point where external force is acting is the bottom left corner of the square."

May it be bottom right corner instead?

yup you are right i typed left instead of right should i repost the problem with better formatting?

 

[pointdexter16]

I can't follow the sketch (so I agree with @berkeman ) but let me ask you two questions:
1. What is the torque on the object?
2. What is its center of mass?

1.to calculate torque we need a point right with respect to which we can calculate torque so what i am trying to achieve is find a point where the torque produced by gravity and external force is zero so that i can consider it as a point through which axis of rotation passes.
2.centre of mass and centre of gravity are the geometric centre of the body

 

[pointdexter16]

Welcome to PF. For future posts, please see the "LaTeX Guide" link below the Edit window. That will help you post math equations here at PF. Thanks.

should i repost

 

[berkeman]

should i repost

You can just add a new post below with your corrections and LaTeX. When you do that let me know, and I'll add a note to your first post to let folks know to skip ahead to the improved/corrected post.

 

[pointdexter16]

I am basing this off on the fact that axis of rotation passes through the point which has a net total of zero torque so in order to find the point i will choose a random point and solve so that the torque produced by gravity and the external force is zero.
things that are give or know:

1.dimensions of the body(square)
2.centre of mass and centre of gravity coincides and are equal to geometric centre
3.point at which the external force is acting
4.theta
5.magnitude and direction of gravitational and external force
6.distance between centre and point on which external force is acting
$r1.g.cos(90-\alpha-\theta)=r2.t.cos(90-\theta+\beta)$
$r1.g.sin(\alpha+\theta)=r2.t.sin(\theta-\beta)$
$r1.g.(sin(\alpha).cos(\theta)+sin(\theta).cos(\alpha))=r2.t.(sin(\theta).cos(\beta)-sin(\beta).cos(\theta))$
$r1.g.((h/r1).cos(\theta)+sin(\theta).(d1/r1))=r2.t.(sin(\theta).(d2/r2)-(h/r2).cos(\theta))$
take r1 and r2 common and cancel
$g.((h).cos(\theta)+sin(\theta).(d1))=t.(sin(\theta).(d2)-(h).cos(\theta))$
$D=d1+d2$
still after substituting values there will be always two unknown variable so there won't be a unique solution

 

[pointdexter16]

You can just add a new post below with your corrections and LaTeX. When you do that let me know, and I'll add a note to your first post to let folks know to skip ahead to the improved/corrected post.

done!!

 

[erobz]

Is the body those two bars?

 

[pointdexter16]

Is the body those two bars?

it's a square in the sketch only the bottom right part is visible

 

[erobz]

it's a square in the sketch only the bottom right part is visible

So the body is just a flat plate?

 

[pointdexter16]

So the body is just a flat plate?

yes with zero thickness

 

[erobz]

yes with zero thickness

So it has no mass?

 

[pointdexter16]

it's not zero but close to that
i took that as the case so that i can solve it in 2D

 

[pointdexter16]

So it has no mass?

if you want you can consider it as a cube but then the the point on which the external force is acting is at the bottom right corner but it's z coordinate is equal to the z coordinate of the centre of the cube such that the torque produced in the z axis is zero

 

[erobz]

if you want you can consider it as a cube but then the the point on which the external force is acting is at the bottom right corner but it's z coordinate is equal to the z coordinate of the centre of the cube such that the torque produced in the z axis is zero

Ok, so you want to ignore the fact that the force is applied out of plane. So its a 2D square with some mass evenly distributed, and a force is acting on its lower right corner. What is the nature of the force e.g. its direction and magnitude? How is it being applied?

 

[pointdexter16]

direction->perpendicular to lower surface, magnitude->t

 

[erobz]

direction->perpendicular to lower surface,

Perpendicular to the lower edge throughout the motion?

magnitude->t

t? ( terrible choice for the name of the force by the way- may I suggest instead $F$) is it a constant magnitude or one that varies in time? Or is it just perhaps an impulsive force ( applied over very short duration of time)?

 

[pointdexter16]

Perpendicular to the lower edge throughout the motion?

t? ( terrible choice for the name of the force by the way- may I suggest instead $F$) is it a constant magnitude or one that varies in time? Or is it just perhaps an impulsive force ( applied over very short duration of time)?

t->thrust
constant

 

[erobz]

t->thrust
constant

Lowercase $t$ is usually reserved for time.

And the direction? Always perpendicular to the lower edge, even as the body rotates?

 

[pointdexter16]

yes its a thruster attached there
ok got the t thing will keep in mind

Lowercase $t$ is usually reserved for time.

And the direction? Always perpendicular to the lower edge, even as the body rotates?

 

[erobz]

As far as I can tell, this is what you are talking about. At some time $t=0$ we have the initial state:

Then at some later time $t$ the system has evolved to:

Is this good?

 

[pointdexter16]

As far as I can tell, this is what you are talking about. At some time $t=0$ we have the initial state:

View attachment 325953

Then at some later time $t$ the system has evolved to:

View attachment 325955
Is this good?

yes but Ft is acting upward

 

[erobz]

and

?

Familiar with Newtons Second Laws?

 

[pointdexter16]

View attachment 325962

and

View attachment 325963

?

Familiar with Newtons Second Laws?

yes

 

[erobz]

yes

Ok, well go ahead and write them down to describe $x(t), y(t), \theta(t)$.

 

[pointdexter16]

Ok, well go ahead and write them down to describe $x(t), y(t), \theta(t)$.

Ok

 

[erobz]

Ok

Turns out I was a little hasty of suggesting to find a closed form for $x(t)$ and $y(t)$. You can write the equations down, but I think it results in some non-elementary integrals involving $\sin \left( kt^2 \right)$, and $\cos \left( kt^2 \right)$...

See: Fresnal Integral

 

[pointdexter16]

Turns out I was a little hasty of suggesting to find a closed form for $x(t)$ and $y(t)$. You can write the equations down, but I think it results in some non-elementary integrals involving $\sin \left( kt^2 \right)$, and $\cos \left( kt^2 \right)$...

See: Fresnal Integral

If possible could you provide me with the whole solution

 

[erobz]

If possible could you provide me with the whole solution

Sorry, No. I can't. But you can write down Newtons Second Laws for the is object and figure out what I'm talking about. Afterword, if you are still curious then take it to the Mathematicians in here to see what they can do with it.