- #1
Moneer81
- 159
- 2
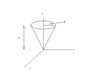
I am trying to understand this example of finding the center of mass of a uniform solid cone.
please refer to the attached figure. We know for obvious reasons that the center of mass will be on the z-axis. I will be referring to the integral that my book used to find the center of mass which is (using the letter S for the integral sign)
R = (1/M) S r dm = (1/M) S k r dV
where R is the position vector, M is the total mass, dm is the element of mass, k is the density, and dV denotes the element of volume.
so for this problem, we have
Z = k/M S z dx dy dz (again, S z dx dy dz means the integral of z dx dy dz)
my first question is how do you evaluate this integral?
thanks
please refer to the attached figure. We know for obvious reasons that the center of mass will be on the z-axis. I will be referring to the integral that my book used to find the center of mass which is (using the letter S for the integral sign)
R = (1/M) S r dm = (1/M) S k r dV
where R is the position vector, M is the total mass, dm is the element of mass, k is the density, and dV denotes the element of volume.
so for this problem, we have
Z = k/M S z dx dy dz (again, S z dx dy dz means the integral of z dx dy dz)
my first question is how do you evaluate this integral?
thanks