Finding the Center of Mass of a Plywood Sheet: A Scientific Approach

[cbarker1]

Dear Everybody,

Shown below is a 4.00-ft by 8.00-ft sheet of plywood with the upper left quadrant removed. Assume the plywood is uniform and determine the x and y coordinates of the center of gravity. Hint: The Earth's gravitational field is also uniform for the entire sheet of plywood.

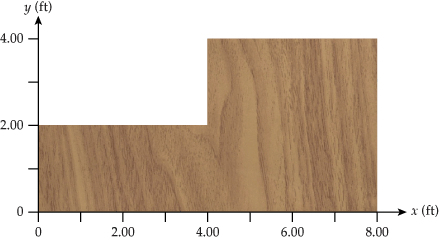
I know the center of mass of the smaller rectangle is at (2,1) and the larger rectangle is at (6,2). I know the density is twice the area of the small rectangle of wood. I need some help with the total center of mass of the object above.

 

[MarkFL]

Let $\rho$ be the uniform mass density of the sheet and $A$ be the area, and so we know:

$$\rho=\frac{m}{A}\implies m=\rho A$$

Now, the find the area, we can define the height $h$ (along the $y$-axis) of the sheet using a piecewise defined function:

$$h(x)=\begin{cases}2, & 0\le x<4 \\[3pt] 4, & 4\le x\le8 \\ \end{cases}$$

Hence:

$$A=\int_0^8 h(x)\,dx=\int_0^4 2\,dx+\int_4^8 4\,dx=2(4-0)+4(8-4)=24$$

And so:

$$m=24\rho$$

Now we need our moments:

$$M_x=\rho\int_0^8 h^2(x)\,dx$$

$$M_y=\rho\int_0^8 xh(x)\,dx$$

What do you find for the moments?

 

[cbarker1]

For the moments in x direction: 80$\rho$ and for y direction 112$\rho$.

 

[MarkFL]

For the moments in x direction: 80$\rho$ and for y direction 112$\rho$.

Yes, I get the same. So now, the center of mass is:

$$\left(\overline{x},\overline{y}\right)=\left(\frac{M_y}{m},\frac{M_x}{m}\right)=\,?$$

 

[cbarker1]

(10/3,14/3)

 

[MarkFL]

(10/3,14/3)

You've got your coordinates reversed...you see $M_x$ is the moment about the $x$-axis and so it is used to find the $y$-coordinate, and likewise $M_y$ is the moment about the $y$-axis, and is used to find the $x$-coordinate.

I made an error in the moment about $x$...it should be:

$$M_x=\frac{\rho}{2}\int_0^8 h^2(x)\,dx$$

This results in the center of mass of:

$$\left(\overline{x},\overline{y}\right)=\left(\frac{14}{3},\frac{5}{3}\right)$$

View attachment 7442