Finding the coefficients of a Resistance vs. Temp curve

[guyvsdcsniper]

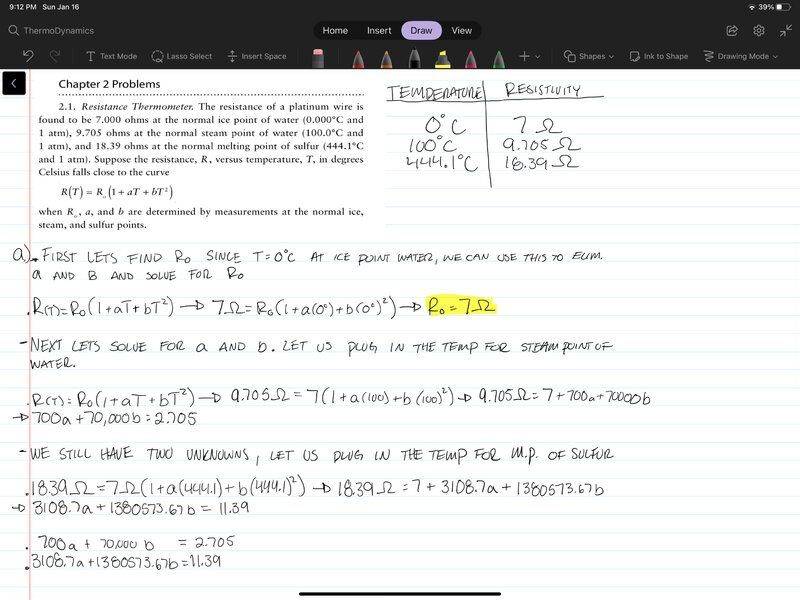
Homework Statement

Find Ro, a, and b.

Relevant Equations

R(T) = Ro (1 + aT + bT2 )

I am asked to find Ro, a, and b. Th problem states the values are determined by the measurements at the normal ice, steam and sulfur points. So I approached the problem by plugging the the temperature problems. For 0°C, Ro reduces to 7 ohms. Then for the other two non zero temperatures, it looks like I am left with a system of equations.

I am a bit stumbled because the values associated for a and b of both equations arent factors of each other, so canceling out seems a bit trickier. I don't really recall running across a problem like this before.

Am I approaching this problem correctly? If so what is a way to solve for a and b?

 

[kuruman]

You have three temperatures which means that you can write three equations, one at each temperature, and three unknowns. The first equation gives you (as you have already found) R₀ = 7 Ω. Use that value in the other two equations which form a system of 2 equations and 2 unknowns a and b. Can you solve that?

 

[guyvsdcsniper]

You have three temperatures which means that you can write three equations, one at each temperature, and three unknowns. The first equation gives you (as you have already found) R₀ = 7 Ω. Use that value in the other two equations which form a system of 2 equations and 2 unknowns a and b. Can you solve that?

I figured it out. I actually just finished a linear algebra course and they never gave us a problem like that where the coefficients weren't perfect factors of each other.

Very noob post. Sorry lol

 

[kuruman]

I figured it out. I actually just finished a linear algebra course and they never gave us a problem like that where the coefficients weren't perfect factors of each other.

Yes, but don't berate yourself. You were led up the garden path. Mathematicians sometimes have a different view of the world from physicists.