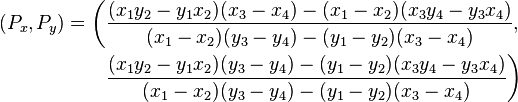Finding the coodinates of two lines.

[animaguy]

I have four points on the same plane (a, b, c, d).

Points a and b form a line ab.

Points c and d form a line cd.

Line ab and cd intersect at point e.

Does anyone have a formula that can find the coordinates of point e?

 

[kanderson]

You would take the midpoint of opposite vertexes. Take the coordinates of A and C, the midpoint of that, then the midpoint of D to B. That is if the plane is say a square with ABCD, listed in order all around. This is if only it is a square. If a parallelogram, I think you take the midpoint A to D, and B to C. I don't really know if my answer is correct, I have geometry teacher that seems sketchy lol.

 

[animaguy]

The problem with this scenario is polygon adcd is not a square or a parrallelogram.

I would be happy if I could find a formula that can determine point e, even if the coordinates were not whole and rounded of.

 

[Evgeny.Makarov]

There is an answer at Dr. Math forum.

 

[I like Serena]

Hi animaguy! :)

From wikipedia (slightly revised to fit the purpose):
The point where multiple lines meet closest in any number of dimensions is:

x= \left(\sum_i I-v_i v_i^T\right)^{-1} \left(\sum_i (I-v_i v_i^T) p_i\right)​

where

$v_i$ is a unit vector along the ith line,
$p_i$ is a point vector on the ith line,
$v_i^T$ is the transpose of $v_i$.​

In your case you have 2 lines and the point where those lines meet closest is the intersection point.
That means:

$v_1 = {b - a \over ||b-a||}$

$p_1 = a$

$v_2 = {d - c \over ||d-c||}$

$p_2 = c$

$x = e$​

 

[animaguy]

Very quickly, I want to thank the help I have received. I am still working out the calculations regarding how I am applying it and so far I am having some problems but it may just be a simple error.

Regardless, thanks for the help and as soon as I have something more concrete to post I will definitely follow up as a courtesy for your help.

(Happy)

 

[animaguy]

``````````````````````````````````````````````````````````````````````````
1)
I used the formula on the wikipedia link provided by ILikeSerena.

Assuming this is the formula that I am genuinely looking for, the two coordinates that I produce by using this formula is not the intersection of the two lines.

2)
And I am still unsure of how to test the revised formula ILikeSerena provided.

3)
I am unsure if the formula provided by the Dr. Math link applies because the formula is based on a three dimensional line.

The two lines are on the same plane (x,y) so a z-coordinate at this point is unnecessary.

```````````````````````````````````````````

Question:

Can anyone provide:

a)
a line with the xy-coordinates of two points on that line

b)
a second line with the xy-coordinates of two points on that line and on the same plane as the first line

c)
and demonstrate the use of a formula using those two lines to produce the intersection of the xy-coordinates of the point at which the two lines intersect?

``````````````````````````````````````````````

I would humbly appreciate it.

``````````````````````````````````````````````

In the meantime, I will keep trying.

Thank you,
Animaguy

 

[I like Serena]

I have just created an excel sheet with 2 lines, using the 2-dimensional formula (from wiki):

http://www.mathhelpboards.com/attachment.php?attachmentid=554&d=1359287603

As you can see, the result matches the intersection point.

The formula I gave is the most generic, which is for m dimensions and for 2 or more lines.
Based on your opening post, I thought you were asking for that.
After your current comment it appears that you don't need it.

 

[animaguy]

I LIKE SERENA,

thanks for the help. i am still having problems solving the formula but I know what the problem is...

(x1 - x2)
(x3 - x4)
(y1 - y2)
(y3 - y4)

are self explanatory for me...

however the values...

x1y2
y1x2
y3y4
y3x4

confuse me...

how are these values defined?

 

[I like Serena]

however the values...

x1y2
y1x2
y3y4
y3x4

confuse me...

how are these values defined?

The expression $x_1 y_2$ means $x_1 \times y_2$.

 

[animaguy]

Problem solved!