Finding the Distance Between Buoys: A Cruise Ship Balcony Problem

[mathdrama]

Not really sure how to do this problem. I'm not even sure where the angles are.

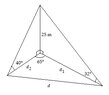
5. The balcony of a cruise ship is 25m above sea level. A person standing on the balcony sees two buoy’s in the water below. The first buoy is situated directly east of her at an angle of depression of 32°. The second buoy is situated 65° south of east at an angle of depression of 40°. Find the distance (x) between the two buoys (B1 and B2) .

 

[MarkFL]

I would begin by drawing a sketch:

View attachment 2514

Now, you can use the Law of Sines to find $d_1$ and $d_2$, and then the Law of Cosines to find $d$, the distance between the buoys.

edit: You could also consider using the tangent function to find $d_1$ and $d_2$.

 

[mathdrama]

I would begin by drawing a sketch:

View attachment 2514

Now, you can use the Law of Sines to find $d_1$ and $d_2$, and then the Law of Cosines to find $d$, the distance between the buoys.

edit: You could also consider using the tangent function to find $d_1$ and $d_2$.

Are attachments acceptable or would LaTex still be more convenient?

Could you kindly help me check my work?

 

[MarkFL]

Posting your work here rather than attaching it is much more convenient for those looking at your work.

One issue I have with what you have done, and it is certainly something I have seen many students do, is using rounded values in your computations. It is better to use exact values until the very end, and only then use a decimal approximation is so desired. Errors from rounding can become compounded if used in intermediary steps.

This is how I would work the problem:

$$d_1=25\cot\left(32^{\circ}\right)$$

$$d_2=25\cot\left(40^{\circ}\right)$$

Now use the Law of Cosines:

$$d^2=25^2\cot^2\left(32^{\circ}\right)+25^2\cot^2\left(40^{\circ}\right)-2\cdot25^2\cot\left(32^{\circ}\right)\cot\left(40^{\circ}\right)\cos\left(65^{\circ}\right)$$

$$d=25\sqrt{\cot^2\left(32^{\circ}\right)+\cot^2\left(40^{\circ}\right)-2\cot\left(32^{\circ}\right)\cot\left(40^{\circ}\right)\cos\left(65^{\circ}\right)}\approx38.4813948\text{ m}$$

You see, using rounded values caused you to round up when the true value should be rounded down. Other than this issue though, your method was correct.