- #1
yazz912
- 45
- 0
1. The problem statement, all variables and given/known
Find the distance from the line
L1: t
2t
3t-1
And
L2: -t+1
t+2
t 2. Homework Equations
Cross product3. The Attempt at a Solution
well I ASSUME that my L1 and L2 were given in parametric equation form Thus L1 would be : x=t y=2t z=3t-1
L2 : x=-t+1 y=t+2 z=t
If I am correct in assuming that,
I then found my vector for L1 u= <1,2,3>
L2 v=<-1,1,1>
Used cross product : uXv
Which I then got n= <-1,4,3>
if I am correct so far... I am stuck on my next step
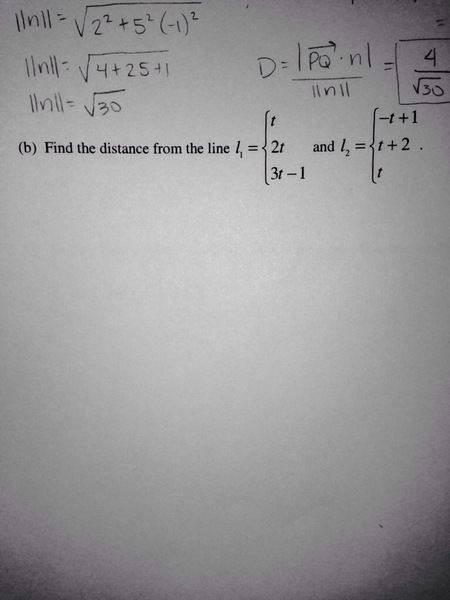
Find the distance from the line
L1: t
2t
3t-1
And
L2: -t+1
t+2
t 2. Homework Equations
Cross product3. The Attempt at a Solution
well I ASSUME that my L1 and L2 were given in parametric equation form Thus L1 would be : x=t y=2t z=3t-1
L2 : x=-t+1 y=t+2 z=t
If I am correct in assuming that,
I then found my vector for L1 u= <1,2,3>
L2 v=<-1,1,1>
Used cross product : uXv
Which I then got n= <-1,4,3>
if I am correct so far... I am stuck on my next step